Onderzoekers ontwikkelen quantumprocessor

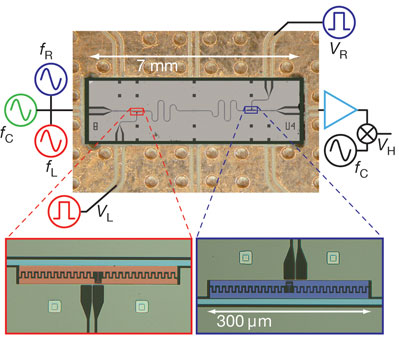
Een groep wetenschappers van de Amerikaanse Yale-universiteit heeft naar eigen zeggen 's werelds eerste solid state quantum-computerchip gemaakt. De processor rekent met twee qubits en is in staat eenvoudige algoritmes af te werken.

De Yale-onderzoekers zijn niet de eersten die een quantumprocessor ontwikkelden, maar ze hebben naar eigen zeggen wel de primeur met de ontwikkeling van een quantum-cpu die gelijkenis met een tradionele processor vertoont. Volgens projectleider Robert Schoelkopf, een natuurkundige die verbonden is aan de universiteit van Yale, is de volledig elektronische quantumprocessor de eerste die eruitziet als een gewone processor en ook zo is te gebruiken. De processor doet zijn werk met twee qubits, die zijn opgebouwd uit miljoenen aluminium-atomen die zich als een enkel atoom gedragen. De twee qubits van de Yale-onderzoeksgroep communiceren met elkaar via een door fotonen gevormde quantum-bus.

Een cruciale eigenschap van de quantum-processor van Schoelkopf en zijn team is de levensduur van de qubits: die kunnen hun quantumtoestand gedurende ongeveer een microseconde vasthouden. Eerdere qubits konden dat slechts nanosecondes. De qubits kunnen daarmee lang genoeg in een toestand van superpositie verkeren om eenvoudige algoritmes, waaronder het Grover-algoritme om databases te doorzoeken en het minder nuttige Deutsch-Jozsa-algoritme, te draaien. De onderzoekers zullen trachten de levensduur verder te verlengen, zodat complexere berekeningen uitgevoerd kunnen worden. Ook zijn ze van plan het aantal qubits uit te breiden, wat de rekenkracht van de processor moet vergroten.

Reacties (49)

Ik snap alleen niet waarom ze de qubits niet kunnen refreshen, werkgeheugen kan ook maar x ms data vast houden maar door om de zoveel tijd even deze opnieuw te setten if( x >= 0.5){ x=1; }else{ x=0;} om het maar even te simpel uit te drukken. Blijft de state langer hoog.

Nu hebben ze qubits en die kunnen ze blijkbaar setten (anders kun je niets uitvoeren). Dus waarom dan niet deze elke keer opnieuw setten, nu snap ik dat dat nu dan wel heel erg vaak moet maar is dat een probleem? Of zit hier nog een complexer probleem aan vast?

Een qubit is een analoge toestand, geen digitale: je zit op een continue schaal. Bovendien, als je hem uitleest gaat hij verloren ("instorten" in het spannende quantumtheoretische jargon ).

Dat is precies wat quantumcomputing zo moeilijk maakt: je kan niet refreshen.

Even ter aanvulling, een quantum staat is in feite gebaseerd op kansen, en de term wavefunction of gulffunctie staat voor de functie die voor elk mogelijke toestand de kans daarvoor definieert. De golffunctie is niet iets dat je uit kunt lezen - je kunt in feite alleen maar kijken of een deeltje zich in een bepaalde stand bevindt en op dat moment wordt de staat ook gekozen - het antwoord is dan simpelweg ja of nee. Dit is afhankelijk van die golffunctie die wordt geevalueerd voor die specifieke staat, en daarmee stort de golffunctie in.

In termen van qubits, met 2 staten (0 en 1), heb je dus een kans dat hij 0 is en de kans dat hij 1 is. Je kunt een qubit bijvoorbeeld zo manipuleren dat hij 70% kans heeft om 0 te zijn en 30% kans op 1. Je kunt aan de qubit niet vragen "wat is de kans dat je 0 bent", maar alleen "ben je 0?". Op dat moment kiest de qubit een staat, en in 70% van de gevallen zal hij dan ja zeggen.

Het mooie van een quantum computer is dat de individuele bits niet per se op zichzelf staan. Oftewel, bij 2 qubits zijn de kansen dat de ene qubit 0 of 1 is ook afhankelijk van de andere qubit. Met 2 qubits zijn er dus 4 mogelijke staten: (0, 0), (0, 1), (1, 0) en (1, 1), ieder met hun eigen specifieke kans. Met 3 qubits worden dat al 8 verschillende staten, en met N qubits zijn er dus 2^N. Vandaar dat de rekenkracht van een quantum processor exponentieel toeneemt met het aantal qubits. Maar denk er wel aan dat een quantum computer geen vervanging is voor een conventionele computer, door het simpele feit dat een quantum computer niet zomaar alle problemen op kan lossen. Maar diegene die hij wel kan, daar is hij meestal een heel stuk sneller in.

Hier staat het ook wel aardig uitgelegd.

[Reactie gewijzigd door .oisyn op 29 juni 2009 14:08]

Maar wat voor antwoord levert een quantum computer dan? Als ik een qubits uitlees is hij 0 of 1... Dat levert me geen informatie over de uiteindelijke toestand op die je systeem had...

Ga je dan bijvoorbeeld 100 keer de berekening uitvoeren, om dan de toestand (=kansverdeling) op die manier te bepalen?

Ja . Het is dan ook noodzaak om je algoritme zo te ontwerpen dat je een minimaal aantal metingen hoeft te doen om een antwoord (met grote zekerheid) te vinden. Quantum algoritmes zijn behoorlijk complex. Een mooi en enigszins begrijpbaar voorbeeld is denk ik Grover's algoritme

Kijk bedankt voor je aanvulling. Ik zag idd het voordeel niet maar met de exponentiële rekenkracht is het volkomen duidelijk!

Als ik het dus goed begrijp zullen we heel misschien in de toekomst een uitbreiding krijgen (ala PCI-E) met een Quantum processor (als ze de communicatie mogelijk kunnen maken) die bepaalde bewerkingen super snel kan uitvoeren? Hiermee doel ik bijv op zoek of encryptie algoritmes.

WAt ik me zou kunnen voorstellen is dat de overhead (het opbouwen en setten van zo'n qubit) langer (of misschien extreem veel langer) duurt dan de levensduur er van.

Hierdoor kan ik me voorstellen dat het totaal nutteloos wordt om te refreshen. MIsschien is het zelfs zo erg dat als ze het wel zouden doen, dat de ontstane CPU langzamer is dan een 8086.

Is quantumcomputing niet de grote vijand van encryptie?

Ja en nee . Het is idd de grote vijand van conventionele encryptie omdat die vaak gestoeld zijn op het product van twee hele grote priemgetallen. Juist het factorizeren van getallen is een erg lastig probleem voor een conventionele computer, en daarom is hedendaagse encryptie relatief veilig (zolang de sleutels groot genoeg zijn). Echter, juist het kunnen factorizeren van getallen is een probleem dat een quantum computer heel makkelijk op kan lossen.

Daar tegenover staat dat de wereld van de quantum mechanica ook mogelijkheden biedt voor nieuwe vormen van encryptie (quantum encryptie), dat, met de huidige kennis van de wetten van QM, onmogelijk te kraken is. Helaas is het momenteel nog wel knap lastig om een goede quantum encrypte verbinding op te zetten tussen twee locaties wegens interferentie tijdens transport.

Grote vijand klinkt een beetje flauw maar inderdaad, door de grote hoeveelheid parallelle berekeningen behoord het sneller kraken van encryptie in de toekomst waarschijnlijk tot de mogelijkheden. Zie ook: http://en.wikipedia.org/wiki/Quantum_computer#Potential

edit: parallelle berekening is niet helemaal het goede woord geloof ik maar geeft volgens mij het beste aan hoe de werking is.

[Reactie gewijzigd door Penalty op 29 juni 2009 13:38]

Symmetrische sleutels zouden teruggebracht worden tot 2^(n/2) complexiteit, dus dat zou nog wel gaan. Maar voor PKI zouden ze dus iets nieuws moeten verzinnen.

nu effe voor de duidelijkheid

de levenduur van de qubit hoeft maar zo lang te zijn als het nodig is om de berekening uit te voeren?

Als een kloktik toch? Voor het tussentijds opslaan van tussenresultaten hebben we toch cache?

Het punt is dat qubits in een superstaat verkeren, en de "tussentijdse resultaten" dus ook. Het is daarbij van belang dat de gehele superstaat wordt gekopiëerd naar een ander deeltje, wat dus niet simpelweg een kwestie is van die staat uitlezen (want daarmee vernietig je de superstaat). Dit is nogal lastig (hoewel niet onmogelijk en er wordt dacht ik ook een hoop research naar gedaan, google maar op Quantum State Transfer), en daar wordt in deze quantum processor nog geen gebruik van gemaakt (er zijn fysiek gezien ook echt maar 2 bits in de "QPU")

[Reactie gewijzigd door .oisyn op 29 juni 2009 13:24]

de levenduur van de qubit hoeft maar zo lang te zijn als het nodig is om de berekening uit te voeren?

Klopt. In het vorige artikel was dat ook niet echt duidelijk. Het staat er ook niet heel duidelijk eigenlijk. Wat men dan ook wil zeggen is de tijd waarin de waarde kan worden vastgehouden. Met deze waarde kan dan worden doorgerekend. Het is dus idd niet de tijd die een quantumprocessor "leeft" tot ie kapot gaat.

erm NEE, hij moet zo lang zijn dat hij de berekening kan uitvoeren plus de tijd waarin hij kan worden uitgelezen. Het "uitlezen" van de superstaat zou deze wel eens kunnen beïnvloeden

Niet "zou wel eens kunnen" - het is per definitie zo dat de superstaat wordt vernietigd bij het uitlezen, omdat er dan een staat moet worden gekozen.

Geef het toch op, quantummechanica is veel te ingewikkeld om op een forum uit te leggen. Alleen dat het, als het werkt, mogelijk wordt om zo'n beetje alle encryptie om te keren en extreme berekeningen te maken met qubits is interessant. Handig dat ze het aan de praat hebben gekregen.

Mischien dat het volgende enigzins kan helpen. Ik ben het zeker met je eens dat om het echt te begrijpen veel meer nodig is dan wat nu volgt (bekend als de Kopenhagen interpretatie).

- De quantumtoestand bepaalt de kans op mogelijke uitkomsten van een meting.
- De quantumtoestand bevat de complete informatie over het systeem (je formule/algoritme).
- Zolang niet wordt gemeten geeft de Schrödinger vergelijking de ontwikkeling in de tijd van de quantumtoestand (je berekening)
- Na de meting is de quantumtoestand ingestort met 100 % kans op de gerealisserde meetwaarde (je uitkomst).
De zaken tussen haakjes zijn een redelijk vrije interpretatie van de algemene quantumfysica naar het hier specifieke geval de "QPU".
De meting geeft je de uitkomst maar heeft als 'side' effect dat de quantumtoestand is 'verbroken' en zich niet meer ontwikkeld.

Je meetinstrument beïnvloed de uitkomst. Daarom kun je maar 1 keer meten. (slaat een beetje op je laatste zin, misschien wel makkelijk om het zo te omschrijven).

ik twijfelde, het is alweer lang geleden dat ik erover bezig ben geweest (het is volgens mij ook quantumfysica als we over de state spreken en quantummechanica als we over de opbouw spreken )

Samen met de quantumcomputer komt echter ook weer het quantumcipher (werkt door middel van de superpositie van fotonen, zie Google), welke theoretisch simpelweg onkraakbaar is, hoeveel rekenkracht je ook hebt.

Neemt niet weg dat quantumprocessors erg snel zijn voor bepaalde processen en dus ook erg nuttig.

Aha dat maakt het net even iets duidelijker, ik heb totaal geen verstand van quantum, maar in het vorige artikel kreeg ik het idee dat het "de tijd die een quantumprocessor "leeft" tot ie kapot gaat."

Maar leuk dat er zoiets gemaakt is, ik ben benieuwd binnen wat voor tijd er daadwerkelijk iets echt nuttigs uit komt.

Als je de wet van moore bekijkt gaat het nog wel even duren voordat hier genoeg rekenpower uit komt. Of krijgen we straks hele clusters quantum cpu's voor berekeningen?

Ben overigens ook benieuwd naar de toestand van deze 'cpu', normaal gesproken moeten materialen volgens mij supergeleidend zijn in quantumcomputers dus heb je extreem lage temps nodig.

De rekencappaciteit stijgt dacht ik exponentieel met iedere toegevoegde qubit. Dat kan dus behoorlijk snel gaan

Nee, de rekencappaciteit stijgt NIET per definitie exponentieel.
Er zijn verschillende berekeningen die een processor kan uitvoeren zoals:
- Optellen
- Aftrekken
- Vermenigvuldigen
- Ontbinden in factoren
- ...

1) Voor een aantal bewerkingen is de qubit ongeschikt (ten opzichte van de normale bit).
2) Zoiets als "Ontbinden in factoren" is iets waar de qubit wel goed in is. De rekencapaciteit voor deze bewerking stijgt wel exponentieel met iedere toegevoegde qubit.

Maar voorverlopig duurt het nog even voordat het equivalent van een Commodore64 in qubits bestaat.

Dat "wetje" is geen natuurwet, maar gewoon een trend die hij zag en zich zo verder gezet heeft.

Helemaal waar, het zou eigenlijk de "bevinding van Moore" o.i.d. moeten heten.

En daarnaast gaat het om het aantal transistoren op een chip, hier gaat het om Qubits. Niet mijn plakje koek, maar een qubit is volgens mij niet echt een (silicium) component.

wow mooi. had dit niet zo snel verwacht.
een tijdje geleden nog een aankondiging waarmee Qubits 1000 keer langer vastgehouden kunnen worden en nu al dit. (heel andere methode maar toch)
sterker nog hij kan standaard algoritmes al gebruiken.

erg mooie ontwikkeling

Die aankondiging was dat de Qubits 4000 keer langer leefde. Bron

Een mooie ontwikkeling! Ik snap ook niet echt waarom ze die Qubits nog langer willen laten leven? Is dit een soort veiligheid zodat ze hun bestemming 100% zeker bereiken?

voor complexere berekeningen is zoals in dit bericht te lezen is de huidige levensduur gewoon niet genoeg.
langere levensduur=complexere berekeningen.

'Ver-duizendvoudigd' - dat is niet 4-duizend volgens mij

Is deze processor met 2 qubits per definitie al sneller dan een ordinaire transistor-type processor?

Nee. Je hebt het equivalent van 2^2=4 traditionele bits. Dit is dus nog vooral een bewijs dat het concept werkt. Met iedere qubit verdubbelt echter het aantal digitale bits dat je nodig hebt om de qubit na te bootsen. Als je zegmaar 32 qubits zou hebben, zou je vier miljard digitale bits nodig hebben om de qubits na te bootsen. En vergelijk ook het aantal operaties: 32 operaties uitvoeren is een stuk minder dan 4 miljard operaties uitvoeren, een kantumcomputer kan, voor de taken waar hij goed in is, potentieel belachelijke snelheidswinsten opleveren.

@dan0s, deze rekenkracht neemt per qubit exponentieel toe volgens mij. M.a.w. met 100 qubits ben je al sneller dan de meeste van onze huidige processoren.

Deze presentatie van de UvA kwam ik een tijdje geleden tegen, geeft duidelijk aan hoe het aantal gelijktijdige berekeningen toe neemt met het aantal Qubits. (vanaf pagina 50)
http://homepages.cwi.nl/~buhrman/paradiso-final.pdf

Is de snelheid van deze processor op een of andere manier te verwoorden met de snelheid waarin we onze huidige processoren uitdrukken? Ik ben benieuwd naar de snelheid, maar qubits zeggen me helemaal niets..

niet zo zeer.
als ik het goed begrepen hebt rekenen quantumprocessoren op een dusdanig andere manier dat veel dagelijkse taken van een normale CPU veel zwaarder zijn voor een quantumprocessor of zelfs gewoon niet te doen, terwijl andere berekeningen gigantisch veel sneller gaan.

er zijn zoooo veel coolere dingen die je met quantum mechanica kan doen. Voor de gene die niet wete nwaar ik het over heb, of die niet vinden dat ze een beeld van quantum mechanica hebben wil ik de documontaire "what the bleep do we know: down the rabbithole" aanraden. een echte eye-opener en volledig wetenschappelijk onderbouwd.

edit: thank you

[Reactie gewijzigd door Anoniem: 185441 op 29 juni 2009 13:40]

"what the bleep do we know" wetenschappelijk verantwoord?! Het is een hele hoop spiritueel geleuter waar ze regelmatig het woord "quantum" laten vallen en verkopen het dan als een "documentaire" over quantummechanica. Enkele bekende wetenschappers die eraan deelgenomen hebben zijn woedend op de makers ervan omdat hun geloofwaardigheid ernstig aangetast is doordat het programma hun woorden volledig uit context genomen heeft. Voor wie er IETS van kent is het ongelofelijk frustrerend om naar de gigantische onzin te kijken die "what the bleep do we know" is.

Wil je echt wat bijleren over quantummechanica en stringtheorie kan ik je The Elegant Universe aanraden: een WETENSCHAPPELIJK programma dat alles voor de gewone mens probeert uit te leggen.

*edit* elegant universe linkt nu direct naar de videos

[Reactie gewijzigd door boe2 op 29 juni 2009 13:45]

En daarnaast is het boek onder dezelfde titel, eveneens van Greene's hand, een echte aanrader. Wel wetenschappelijk verantwoord en verbazingwekkend

Nu is de What The Bleep Do We Know serie niet echt bijzonder uitmuntend te noemen, lees eerder een aantal goede boeken over quantummechanica, is misschien lastiger maar daar heb je meer aan dan dat je een semi-wetenschappelijke documentaire bekijkt...

on-topic:

Interessant om te zien dat toepassingen op dit gebied snel opvolgen, ook al betekent dit natuurlijk niet dat we moeten denken dat we over 5 jaar allemaal een quantumcomputer thuis hebben staan.

@ dan0s: Moore's Law gaat niet op bij quantumcomputers, rekenkracht neemt exponentieel toe bij iedere extra qubit.

[Reactie gewijzigd door Farscape2 op 29 juni 2009 12:54]

Die serie is half wetenschappelijk en half new-age/filosofisch gewauwel. Ik geef toe dat het leuke stof tot nadenken geeft, maar neem er aub niet alles klakkeloos van over.

en ontopic:
Ik zie in het diagrammetje dat het ding met gewone spanning wordt aangestuurd. Verder wordt er vermeld dat het als een 'gewone' cpu te gebruiken is.... En het zou simpele dingen als het Grover-algoritme moeten kunnen doen. Leuk, maar hoe? Kunnen we al een PCI-E kaartje met zo'n ding kopen? Ik mis wat vermeldingen van termijnen enzo....

"The Elegant Universe" is een veel betere serie, door de bekende natuurkundige Brian Greene. Overigens gratis te bekijken online (in delen).

Das een hele enge serie.
Waarin uiteindelijk blijkt, dat we onderdeel zijn van 'niets'

wat is nu het nut van zo iets? ik begrijp deze quantum berichten nooit. Gaat dit nu altijd om de snelheid? Waar dienen de quantumcomputers voor?

Quantumcomputers zijn zeer sterk in het oplossen van specifieke wiskundige problemen. Zij kunnen deze berekeningen maken op zeer korte tijd, waar een "gewone" computer weken/maanden zou bezigzijn.

Quantum computers kunnen bepaalde berekeningen in een stap doen, waar een traditionele berekening zeer veel stappen nodig heeft.

Ikzelf vind de vergelijking met complexe getallen een goede, waar ik voor de traditionele Euler berekening een kantje nodig had voor een vermenigvuldiging, met (Fourier getransformeerd of Laplace, het is weer lang geleden) waren het 2 regeltjes. Of analoog, beschrijf een bol met behulp van Carthesische of bol-coordinaten.

Je kan beide methoden gebruiken alleen de ene methode is veel omslachtiger.

De toepassingsgebieden zijn zeker voor quantummechanica goed.. denk eens in hoe snel een programma als Gaussian voor complexe moleculen dan klaar zou zijn. Andere gebieden vast ook, maar dat kan een wiskundige vast beter vertellen dan ik.