Onderzoekers bouwen organisch ternair geheugen

Door trits in plaats van bits te gebruiken, denken Chinese onderzoekers de capaciteit van geheugen verder op te kunnen schroeven. Het ternaire geheugen dat zij hebben ontwikkeld, is gebaseerd op organische moleculen.

De Chinese onderzoekers hebben een prototype van het organische ternaire geheugen gebouwd dat slechts eenmaal beschreven kan worden. Wel kan het geheugenprototype meermalen worden uitgelezen, maar de wetenschappers van de Soochow-universiteit willen het geheugen uiteraard herschrijfbaar maken. De opslagcapaciteit van geheugen zou bij gelijkblijvende afmetingen vergroot kunnen worden als er trits in plaats van bits worden gebruikt, waarmee niet twee, maar drie verschillende waarden kunnen worden opgeslagen.

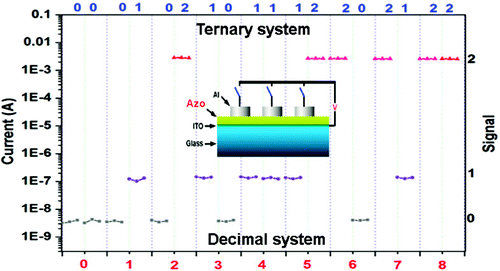
Het ternaire geheugen dat door Hongwei Gu en Jianmei Lu werd ontwikkeld, bestaat uit een organische verbinding die tussen elektrodes van aluminium en indium-tinoxide wordt aangebracht. Door spanning op de elektrodes te zetten, verandert de mobiliteit van elektronen in het organische materiaal. Het is mogelijk om voor een lage, gemiddelde of hoge mobiliteit te kiezen, wat correspondeert met de ternaire toestanden 0, 1 of 2. Het gebruik van trits voor praktische doeleinden staat overigens nog in de kinderschoenen: de meeste ternaire systemen zijn experimenteel van aard.

Reacties (74)

[naam]

Als dit eenmaal goed ontwikkeld is en werkt dan is dat denk ik zo een beetje het begin van een hele nieuwe generatie computers. Geen binair systeem maar een trinair systeem..

[.oisyn]

Onzin, computers blijven gewoon binair, simpelweg omdat een ternair systeem niet praktisch is. Het enige wat deze doen is een geheugencel 3 staten geven zodat er meer informatie in past. Uiteindelijk komen er gewoon weer bits uitrollen (en voor een 64 bits getal heb je dan niet meer 64 maar 41 cellen nodig)

[Reactie gewijzigd door .oisyn op 22 juli 2024 23:20]

[cPT.cAPSLOCK]

Nee, dat is onzin.

bedenk eens:
als je 8 schakelaartjes hebt met 2 mogelijke waarden, geeft dat 2⁸ combinaties = 256 combinaties.

3⁸ is al 6561 mogelijkheden.

Dat is meer dan 25 keer zo veel, en dit verschil wordt exponentieel groter per schakelaartje.

Het probleem was echter dat als je een bit een 3e waarde wil geven (schakelaartje in het 'midden' zetten) deze vaak door schoot in plaats van in het midden te blijven staan. Dat is met deze techniek geen probleem.

Op een tertiair systeem overstappen is absoluut the way to go, maar op dit moment praktisch onuitvoerbaar.

[Reactie gewijzigd door cPT.cAPSLOCK op 22 juli 2024 23:20]

[iMispel]

Nee hoor, wat .oisyn zegt is volledig juist:
De berekening die hij hier voor gebruikt is de volgende:

• voor 64 bits: log(2^64)/log(3) = 40,3795 => 41 trits
• voor 32 bits: log(2^32)/log(3) = 20,1898 => 21 trits
• voor 16 bits: log(2^16)/log(3) = 10,0949 => 11 trits
• ...

Dit is mooi lineair en blijft lineair, punt. Maakt niet uit hoeveel bits. Waar het op neer komt is: om een aantal bits voor te stellen in trits heb je slechts +/- 63% van het aantal cellen nodig. formule hiervoor: log(2)/log(3) (vrijs simpel dus).

Je vergelijking van 2^8 met 3^8 die een verschil van factor 25 opleveren slaat werkelijk op niets. Als mijn buurman een schijf heeft van 4000Gb (500GB) en ik van 8000Gb (1000GB), dan heb ik dubbel zoveel geheugen, kan ik dubbel zoveel films foto's MP3's opslaan. en niet 2^4000000000000 zoveel. Het feit dat ik een factor 2^4000000000000 meer combinaties kan maken met mijn schijf doet totaal niet ter zake.

Het komt er op neer dat als een trit minder dan 1,58 keer de fysieke plaats van een bit inneemt er meer geheugen per oppervlak mogelijk is, anders simpelweg niet.

BTW: True or false: 1 of 0, Execute or non-execute: 1 of 0. OR AND en andere logische bewerkingen met trits??? Dit systeem lijkt me sowieso alleen maar handig om geheugen opslag te realiseren.

[Reactie gewijzigd door iMispel op 22 juli 2024 23:20]

[zenlord]

Bah neen - alles gewoon herschrijven naar IF ... THEN :-)

[robvanwijk]

Op een tertiair systeem overstappen is absoluut the way to go, maar op dit moment praktisch onuitvoerbaar.

Ternair heeft wel voordelen, het mapt bijvoorbeeld prima naar fuzzy logic: true, false, maybe. Maar denk er wel even aan dat je schakelingen dan ook fors ingewikkelder worden! En dat we een paar decennia aan ontwerp-ervaring (à tientallen (honderden?) miljarden euros) opnieuw bij elkaar mogen werken. Dus of het "the way to go" is...? In elk geval niet op korte of middel-lange termijn.

[Makine_31]

Dat lijkt mij meer op de kwantumtechnieken waar hierboven over gesproken wordt met 0 en 1 en alles ertussen, false true en alles ertussen (maybe) en niet het 0, 1 en 2.

Ik geloof ook wel dat dit een goede ontwikkeling is, echter omdat het nog ver in de babyschoenen staat duurt het nog heel lang voordat het rendabeler wordt als het huidige binaire systeem.

[Reactie gewijzigd door Makine_31 op 22 juli 2024 23:20]

[robvanwijk]

Nee, dit heeft niks met quantumcomputers te maken. Daar hebben (setjes van) bits alle mogelijke waarden, tegelijk. In een (binaire) quantumcomputer die werkt met getallen van 3 bits zal elke waarde dus zowel 000b, 001b, 010b, ... als 111b zijn. In een (ternaire) quantumcomputer die werkt met getallen van 3 trits zal elke waarde dus zowel 000t, 001t, 002t, ... als 222t zijn. Dat is compleet anders dan in een normale computer.
Wat ik in mijn vorige post zei over fuzzy logic moet je zo lezen:
In een binarie computer worden waarden voorgesteld met nullen en enen. Als die waarde een getal is, dan is dat gewoon via een binaire representatie. Als het echter een logische waarde is, dan kun je "omrekenen" via 0 -> false, 1 -> true.
In een ternaire computer worden waarden voorgesteld met nullen, enen en tweeën. Als die waarde een getal is, dan is dat gewoon via een ternaire representatie (voorbeeld: 201t = 2 * 3^2 + 0 * 3^1 + 1 * 3^0 = 18 + 0 + 1 = 10). Als het echter een logische waarde is, dan kun je "omrekenen" via (bijvoorbeeld) 0 -> false, 1 -> maybe, 2 -> true (of juist via 0 -> false, 1 -> true, 2 -> maybe als je dat handiger vindt).
Net zoals je in Boolse algebra kunt zeggen False OR True = True (0 OR 1 = 1), False AND True = False (0 AND 1 = 0), True AND True = True (1 AND 1 = 1), zo kun je in ??? algebra zeggen False OR Maybe = Maybe, Maybe OR True = True, Maybe AND True = Maybe, etc. (over de XOR zou ik iets langer na moeten denken of opzoeken).
De wiskundige kant hiervan is helemaal zo'n probleem niet, maar met driewaardige geheugencellen ben je er niet, je moet ook driewaardige logische schakelingen gaan maken en dat kan wel eens iets lastiger zijn, want dat staat inderdaad nog wel in de kinderschoenen. Of "rendabeler" het goede woord is weet ik niet... Het lijkt mij dat binaire en ternaire computers ieder goed zijn in bepaalde dingen. Als ze daarin ver genoeg boven de ander uitsteken dan zitten we straks met een situatie waarin je bij elke computer eerst moet kijken of ie binair of ternair is...

@ .oisyn: Je hebt helemaal gelijk. Omdat ik vooral uit wou leggen waarom ternair rekenen iets heel anders is dan quantum rekenen heb ik de bocht inderdaad wat afgesneden. Bedankt voor de aanvulling!

[Reactie gewijzigd door robvanwijk op 22 juli 2024 23:20]

[.oisyn]

Daar hebben (setjes van) bits alle mogelijke waarden, tegelijk. In een (binaire) quantumcomputer die werkt met getallen van 3 bits zal elke waarde dus zowel 000b, 001b, 010b, ... als 111b zijn

Da's ook wat kort door de bocht. Waar het om gaat is dat een set qubits zich in een quantum staat bevinden waarbij ze feitelijk idd elke mogelijkheid kunnen zijn, maar daaraan gekoppeld zit ook een kans voor elke specifieke mogelijkheid. Het is dus niet zonder meer waar dat een qubit altijd zowel 0 als 1 is. Als de kans 100% is dat hij een 0 is zal hij immers geen 1 zijn.

Pas bij het uitlezen (het observeren) wordt er een staat aangenomen. Er is dus geen mogelijkheid om direct de hele quantum staat en bijbehorende kansen te bepalen. Het enige wat je kunt doen, is de berekening keer op keer overnieuw doen, en aan de hand van de verschillende antwoorden die je krijgt bepalen wat de kansen waren. Hierdoor is een quantum computer ook geen heilige graal oid, voor conventionele berekeningen is hij gewoon heel slecht. Maar bepaalde problemen die voor een conventionele computer heel lastig zijn, zoals bijv. het factorizeren van een getal, kan een quantum computer heel snel oplossen.

[reefclaw]

En hoe zou je binaire data dan ternair op kunnen slaan?
Het enige wat ik dan zou kunnen bedenken is dat elke x bits gelijk is aan y cellen, bijvoorbeeld met 4 bits = 3 cellen:

0000 = 000
0001 = 001
0010 = 002
0011 = 010
0100 = 011
0101 = 012
0111 = 020
1000 = 021
1001 = 022
1010 = 100
1011 = 101
1100 = 102
1101 = 110
1110 = 111
1111 = 112

[RielN]

Als dat wordt opgeslagen zoals een CD is het efficienter, soort kanaalcodering naar tertiare waardes.

Bovendien als je elke drie bits omzet naar twee ben je efficienter

Spaar je 33% ipv 25%

000 = 00
001 = 01
010 = 02
011 = 10
100 = 11
101 = 12
110 = 20
111 = 21

22 houd je over. Ziet gek uit...?

[Reactie gewijzigd door RielN op 22 juli 2024 23:20]

[iMispel]

Nee, ziet er niet gek uit: met 3 bits ben je al behoorlijk efficient: (3/2)/(log(3)/log(2) = 94,6%
Je hoeft het echter niet allemaal manueel uit te rekenen hoor:
Als in excel in de eerste kolom 1, 2, 3, enz invult en in de 2de kolom =(A1/AFRONDEN.BOVEN(LOG(2^A1)/LOG(3);1))/(LOG(3)/LOG(2))
invult (en deze doorrekken naar beneden natuurlijk) krijg je als resultaat de procentuele efficiëntie van het aantal bits dat je wil packen naar een antal trits tegenover het theoretisch maximum (=36,91%). Enkele voorbeelden (met ook het aantal trits bij):
# bits # trits Efficiëntie

1 bits => 1 trits 63,09%
2 bits => 2 trits 63,09%
3 bits => 2 trits 94,64%
4 bits => 3 trits 84,12%
16 bits => 11 trits 91,77%
32 bits => 21 trits 96,14%
41 bits => 26 trits 99,49%
84 bits => 53 trits 99,996%
128 bits => 81 trits 99,70%

[Reactie gewijzigd door iMispel op 22 juli 2024 23:20]

[Verwijderd]

Het voordeel van 3bits=>2trits is dat de mapping heel eenvoudig is. Om met de super efficiente 84b=>53t te werken heb je een logische "poort" nodig die 53 ingangen heeft.
Een ander voordeel van de extra toestand is dat bijvoorbeeld "leeg" en "nul" onderscheiden kunnen worden, of bad-cell markering gebruikt kan worden.
In het tijdperk van 128 bit code kan er natuurlijk wel winst gemaakt worden met de compressie in 81 trits, maar ik denk dat die winst niet opweegt tegen de eenvoud van 129b=>86t door 43 setjes van 3b resp 2t te nemen. (Kan je die ene bit ook weer ergens speciaal voor gebruiken)

[Verwijderd]

Je zou natuurlijk ook naar de grafiek bij het artikel kunnen kijken.....

edit ter verduidelijking: Waar de trits dus wel degelijk per paar gebruikt worden.

[Reactie gewijzigd door Verwijderd op 22 juli 2024 23:20]

[Plasma_Wolf]

Zoals je zelf hier al laat zien, gebruik je niet elke mogelijke waarde van je drie trits. Dat is geen probleem bij het converteren van binaire data naar ternaire data, maar wat als ik de data dan met een ternaire computer wil bewerken.

Ook dat is wel mogelijk, maar als we bijvoorbeeld 212 krijgen, moeten we dat eerst terugconverteren, door er een trit bij te plaatsen. Zo wordt het misschien wel 100+112, wat je vervolgens naar binair converteert. Dat wordt dan 1010+1111. Als ik het goed berekend heb is dat 011101 (twee bits toegevoegd). Op deze manier kun je een bestand dat in bits is gemaakt, toch overzetten en uitlezen als trits.

Voor zover is het wel mogelijk, maar ik vraag me af hoe het moet met het verwerken van data over het internet. Iedere ternaire computer moet, vanwege de huidige staat alle data converteren om requests te zoeken.

Ik denk dat dat evenveel werk kost als je winst in geheugen en, als het mogelijk is met verdere ontwikkeling, een ternaire processor (dan heb je en volledig ternaire computer, in plaats van een pc met alleen ternair geheugen).

Het converteren lijkt mee een behoorlijk intensieve klus (ook al is het misschien niet moeilijk), dit komt om dat 2ⁿ != 3ⁿ.

[AugmentoR]

En hoe zou je binaire data dan ternair op kunnen slaan?

zo dus:
000 = AAA
001 = AAB
010 = AAC
011 = ABA
100 = ABB
101 = ABC
110 = ACA
111 = ACB

edit:
beetje laat, beetje dubbel

[Reactie gewijzigd door AugmentoR op 22 juli 2024 23:20]

[Verwijderd]

Mja, en de eerste letter blijft telkens een A en bevat dus geen informatie, die kan je dus weglaten zonder informatie weg te gooien

[Verwijderd]

Een binair getal omrekenen naar ternair is net zo evident als omrekenen naar een decimaal of hexadecimaal getal. Bijv het decimaal getal 25:

binair: 11001
hexadecimaal: 19
ternair: 221

Het was eventjes puzzelen maar een computer heeft dit natuurlijk zo omgezet. Voor dataopslag maakt het dus niets uit welk getallenstelsel je gebruikt. Desnoods laat je dit omzetten in bijv de drive zelf zodat de computer er niets van merkt. Zo hebben we ooit een keer een stuk meer opslagruimte in drives van fysiek dezelfde grootte.

[Reactie gewijzigd door Verwijderd op 22 juli 2024 23:20]

[BramT]

Hmm, dat is wel erg conservatief gedacht. Ik kan me een ternaire schakeling voorstellen die per kloktik meer informatie kan verwerken dan een binair systeem...

Ben niet erg thuis in die wiskundige systemen, maar kijk bv wat ze voor kunstjes kunnen uithalen met geavanceerde paritychecks (PAR2)...

[thommich]

Is dat niet ook waar ze met kwantumtechnieken mee bezig zijn??

Verder is de implementatie ervan dan wel opeens veel moeilijker dan binair dacht ik.

[Verwijderd]

Nee dit is iets anders, een kwantum computer heeft een qubit. Deze heeft een state die zweeft tussen 0 en 1 .

[postbus51]

Een kwantumcomputer heeft kwantumbits, meestal qubits genoemd. Die hebben ook twee toestanden, maar kwantumbits kunnen in beide toestanden tegelijk verkeren

de bekende Q toestand is pas na waarneming bekend en vast

[analog_]

En dan ook niet meer aanwezig doordat je met de observatie een verandering hebt aangebracht. Enfin das het huidige probleem oa.

[Sn3akz]

"Kat in the box" paradox

[Verwijderd]

Bedoel je dat het niet 0 of 1 of 2 is maar 0 of (1 of 2) ?

[thommich]

Ik ben helemaal niet op de hoogte van kwantumtechnologie, maar ik dacht dat het in se ook een trinair systeem was, omdat er 3 verschillende toestanden mogelijk zijn per element van het systeem?

[sjaakwortel]

nouja, 2 toestanden maar ze kunnen ook tegelijk dus 0,1,01
klopt inderdaad

[Verwijderd]

Ik denk dat trinair hier gewoon puur een coderingsmechanisme is om meer data kwijt te kunnen op de dezelfde oppervlak. Er zal in de praktijk heus wel iets van een TDC (Trigital to Digital Converter) of iets in die geest gebruikt worden.

[Reactie gewijzigd door Verwijderd op 22 juli 2024 23:20]

[ls470]

Niet echt denk ik. hun ternair geheugen betekent dat ze 3 verschillende waarden in hun geheugen (dat een analoog medium is) kunnen steken ipv er maar 2 te gebruiken. In Flash geheugens wordt dit al veel langer gedaan met het verschil dat ze proberen machten van 2 te gebruiken (4 waarden per cel is het klassieke 2bit/cel MLC geheugen, maar 8 en 16 waarden per cel worden tegenwoordig ook al gebruikt) omdat dat de controller iets simpeler maakt.

[Dutchman140]

Ik was laatst op de universiteit in Eindhoven. Daar heb ik met een aantal laatste jaar studenten gepraat. Deze zeiden dat het tegenwoordig theoretisch wel al mogelijk was, maar er nog heel wat problemen waren ivm het upgraden. Want momenteel is alles binair in de ICT wereld. Als je alles moet upgraden naar trinair, dat gaat nog heel wat tijd kosten, en vooral geld. Nu weet ik natuurlijk niet wat er precies alles speelt omdat ik zelf verder geen studie in die richting doe.

Natuurlijk, het zal langzamerhand gaan, maar er zullen toch nog genoeg problemen komen.

Natuurlijk juich ik zulke ontwikkelingen wel toe en ik hoop ook dat we hier ooit naartoe werken. Want dit is, zoals je zegt, toch een hele nieuwe generatie computers.

[Reactie gewijzigd door Dutchman140 op 22 juli 2024 23:20]

[Paul - K]

Ben erg benieuwd hoe dit zal gaan uitpakken...
Betekent dit dan ook dat je geen binair systeem heb maar trilinear ofzo? Hoe simpel gaat is dit te 'integreren' ?

[DominoNL]

Kan me voorstellen dat je in een Ternaire opslag ook gewoon binair op kan slaan, door gewoon stand 2 niet te gebruiken. Moet je alleen aan het begin van een software protocol even aangeven wat er gaat gebeuren! =P..

[Paul - K]

Wat zou je er dan aan hebben? Kost alleen maar meer...

[cPT.cAPSLOCK]

Waarschijnlijk komt er een controller tussen die de binaire dat omzet van binair naar tertiaire data bij het schrijven, en van tertiair naar binair hij het lezen. Dan heb je dus meer capaciteit in dezelfde ruimte, bruikbaar met huidige systemen.

Vraag me alleen af of zo'n vertaal-chip de snelheden te pas gaat komen.

[Reactie gewijzigd door cPT.cAPSLOCK op 22 juli 2024 23:20]

[stappel_]

of gewoon een "dual channel geheugen"

trinair 1 == bit 1 + bit 2
trinair 2 == bit 3 + bit 4
etc

[Robby517]

Aangezien trinair 3 staten kent en binair 2 kan jouw voorbeeld toch niet kloppen, bit 1 + bit 2 = 4.

[Rauzi]

Je zou een slimme manier van nullen en enen opslaan kunnen maken. Zoiets als

ternair 0 = 00 binair
ternair 1 = 01 binair
ternair 2 = 10 binair

om dan binair 11 te maken kun je c(0) nemen, met c de functie die "het complement" neemt van de binaire representatie. kost dus iets meer rekenwerk maar het kost minder opslag! een string als

00111010101110100011 binair wordt dan 0c(0)222c(0)220c(0) ternair, 20 symbolen binair tegenover 10 symbolen ternair + 3 cpu operaties.

je kunt op zoveel manieren alles gewoon binair blijven schrijven in de software wereld dus, mocht er ooit een ternair opslag systeem komen.

[DataGhost]

Hoe was je van plan die c(0) op te gaan slaan dan?

Verder kan je allang gewoon omrekenen van binair naar trinair of welk talstelsel dan ook.

[michaelmou]

Organische moleculen zijn koolstof, waterstof, zuurstof, stikstof en zwavel. Dit wil niet zeggen dat het geheugen van planten zijn gemaakt of zo.

[gnimmeL_kraD]

Ik denk dat de meeste hier ook wel zoiets globaal weten, maar het blijft leuk om te geinen over levende machines enzo

[postbus51]

dus niet elementen koolstof , waterstof , zuurstof

[grobbel]

Ik wordt oud...
Was er een jaar of 40 geleden niet al ergens in Rusland(?) een computer systeem met 3 niveaus?

[Decalies]

Weet ik niet, maar het idee/onderzoek naar ternaire systemen is inderdaad al zeker een aantal decennia oud.

[HerrPino]

Dat was ook mijn eerste gedachte, en ik heb hem gevonden dat was de Setun uit 1958

bron: http://en.wikipedia.org/wiki/Setun
en nog 1 eerder in 1840: http://en.wikipedia.org/wiki/Ternary_computer

[Reactie gewijzigd door HerrPino op 22 juli 2024 23:20]

[Quacka]

Ik dacht dat oude mensen altijd zeggen dat het onderwijs vroeger zoveel beter was.
Ik denk dus niet dat jij zo oud bent.

omtopic: Ik geloof dat ik te dom ben voor dit nieuws. Ik begrijp er niet veel van.
Tegen de tijd dat het echt toegepast zal gaan worden zullen er wel mensen zijn die het goed kunnen uitleggen. Hoop ik dan maar....

[Reactie gewijzigd door Quacka op 22 juli 2024 23:20]

[Verwijderd]

Als je begrijpt hoe binaire opslag werkt dan is het ternaire principe niet zo lastig omschakelen. Je gaat van bits naar trits dus ieder geheugen-element kan niet in 2 maar 3 staten bestaan. Bits kunnen 0 of 1 zijn, trits 0, 1 of 2. Zo kunnen 2 bits samen maximaal 2 x 2 = 4 staten vastleggen maar 2 trits 3 x 3 = 9 staten. Anders gezegd: als je een getal vastgelegd met trits omrekent naar een getal vastgelegd in bits dan heb je ineens veel meer geheugen-elementen nodig om het grotere aantal bits op te kunnen slaan. Met trits bespaar je dus op fysieke opslagruimte.

Neem ook het voorbeeld dat eerder postte:

Een binair getal omrekenen naar ternair is net zo evident als omrekenen naar een decimaal of hexadecimaal getal. Bijv het decimaal getal 25:

binair: 11001
hexadecimaal: 19
ternair: 221

Voor het getal 25 heb je dus 5 bits nodig maar slechts 3 trits. En 2 geheugen-elementen als je een decimaal of hexadecimaal stelsel gebruikt maar dat is voor opslagredenen niet relevant.

[Reactie gewijzigd door Verwijderd op 22 juli 2024 23:20]

[DrPoncho]

Is dat zoiets als dit;

http://www.zdnet.nl/news/114798/hp-toont-revolutionaire-memristor-chip/

[Wafje]

verwijs liever naar een link uit deze site :
nieuws: HP ontwikkelt nieuw geheugenelement

En neen, dit is het zeker niet.

Terniar gegeugen vergroot de capaciteit van het gegeugen (meer gegevens voor gelijke oppervlakte beschreven). Die memristor kan ternair, binair of zelfs hexadecimaal zijn, de beste manier moet nog worden ondekt.

[Relief2009]

Hoezo zou hij naar een link verwijzen die 2 jaar ouder is? Die link is een stuk nieuwer en gaat waarschijnlijk over de vorderingen.

In jouw link hebben ze het over een ontwerp en in die laatste link over realisatie. Big difference.

[Verwijderd]

Organisch? Lijkt me nogal kwetsbaar voor schimmels en andere ehm.. bugs

[Thomas M]

Organisch betekend dat er koolstof en soms wat zuurstof en waterstof in de stof zit.
Bijvoorbeeld benzine is ook organisch of plastics, die zijn ook organisch of et cetera.
Het komt eigenlijk van "organische chemie" dat een zeer veelomvattend vakgebied is.

[tehsojiro]

ik moest bij het woord 'organisch' denken aan rode stukken kloppend vlees met chipjes en draadjes erin

[Verwijderd]

Het leeft?

[Wafje]

nee, organisch wil gewoon zeggen dat de gebruikte stoffen verbindingen zijn mdiekoolstofatomen bevatten.

[Verwijderd]

Bijna goed. Organische moleculen bevatten volgens de norm meerdere koolstofatomen, doorgaans meer dan 3 maar dat nummer is wel enigszins arbitrair. Zo zijn kooldioxide, ethanol en aceton bijvoorbeeld nog anorganisch.

[Verwijderd]

Zo zie je maar dat Dick Maas zijn tijd ver vooruit was met De Lift!

[Verwijderd]

offtopic:
lol, ik denk dat dit er nog meer naartoe gaat.

[Verwijderd]

Ik vraag mij af wat ik mij kan voorstellen bij deze zin: " ... het organische materiaal ... " ?
Is het een cel? Groepje cellen? Een (stukje) labrat?

[hotrid]

Het is organisch vanwege het feit dat het uit een azzo-onderdeel bestaat. Een azzo-molecuul bestaat uit R-N=N-R', waarbij de restgroepen (R en R`) aluminium en indium tin oxide. Deze gebruikte restgroepen functioneren dan als electroden, waarbij telkens de geleidbaarheid kan veranderen, waardoor er 3 dimensies beschikbaar zijn. Theoretisch gezien zal deze methode nog ver in de kinderschoenen staan, omdat het bij meerdere componenten/schakelingen de geleidbaarheid en dus de wisseling van de 3 dimensies moeilijk is te regelen.

[Bartjezz]

Hmmm, interessante ontwikkeling! Hopelijk houdt het geheugen dan ook de waarde 1/2/3 vast, niet dat na verloop van tijd de 3 verloopt naar een 2 ofzo... Maar als deze techniek wordt doorontwikkeld, krijg je gemakkelijk een usb stick met 1TB flash geheugen...