Wetenschappers hebben algoritmes voor quantumcomputersimulaties ontwikkeld die efficiënt kunnen draaien op gedistribueerde systemen. Met klassieke computers kunnen ze zo meer qubits simuleren dan aanvankelijk gedacht.
De onderzoekers van Google draaiden hun simulatie op virtuele machines van Googles Cloud Compute-platform. "Ons gebruik van bescheiden computerhardware democratiseert quantumsimulaties", stellen ze in hun onderzoek.
Simulaties van quantumcomputers gebeurt meestal op supercomputers, vanwege het complexe rekenwerk. Dat is met name vanwege de snelle interconnects die de systemen in een rekencluster van supercomputers met elkaar verbinden. De algoritmes van de wetenschappers hebben dergelijke interprocess communication niet nodig, waardoor ze ingezet kunnen worden op gedistribueerde clusters, zoals die van cloudplatformen.
Een van de voordelen die dit oplevert, is dat de enorme geheugenhoeveelheden die nodig zijn voor quantumsimulaties op supercomputers, niet nodig zijn. In 2016 voorspelden onderzoekers, eveneens van Google, dat het simuleren van circuits van meer dan 48 qubits met hoge diepte, van zo'n 40 lagen, met de supercomputers van toen onmogelijk was. Voor het draaien van de algoritmes op een circuit van 6 × 8 qubits zou 2,252 petabyte werkgeheugen nodig zijn, betoogden ze. Vanwege die praktische grens sprak Google van 'quantum supremacy': het punt waarop klassieke computers niet meer toereikend zijn wat betreft simulaties en quantumcomputers hun klassieke evenknie voorbijstreven.
Bij het huidige onderzoek voerden de wetenschappers echter op het Cloud Compute-platform een simulatie van een raster van 7 × 8 qubits en diepte van 40 lagen uit. Dat vergde 'slechts' 16TB aan ram en de kosten schatten ze op 35.184 dollar. Hun techniek is schaalbaar naar complexere circuits: ze schatten dat quantumcircuit van 7 × 7 qubits met diepte van 48 lagen zo'n miljoen dollar kost.
De diepte betreft het aantal lagen waarin een circuit opgedeeld kan worden zonder dat de gates voor de qubits elkaar overlappen, oftewel, hoeveel logische operaties geïmplementeerd kunnen worden. Het rekenwerk dat quantumcircuits kunnen verrichten wordt bepaald door rasters van qubits in combinatie met die diepte. Het simuleren van grote aantallen qubits met geringe diepte op klassieke computerarchitectuur is al langer mogelijk.
De uitkomsten van de simulaties zoals de onderzoekers die voorstellen zijn wel bij benadering, maar dat geldt voor echte quantumcircuits ook. Qubits vertegenwoordigen anders dan gewone bits niet ofwel de waarde 0 ofwel een 1, maar kunnen tegelijkertijd een 0 en 1 aannemen. Het aantal verschillende waarden neemt exponentieel toe met het vergroten van het aantal qubits. Een quantumcomputer kan zo in een keer parallelle berekeningen uitvoeren en direct tot een definitieve uitkomst komen, bijvoorbeeld door alle uitkomsten in een keer na te gaan waarbij alleen de juiste overblijft. Wetenschappers wereldwijd experimenteren met dit gegeven om een quantumcomputer te ontwikkelen die in te zetten is voor daadwerkelijk rekenwerk.
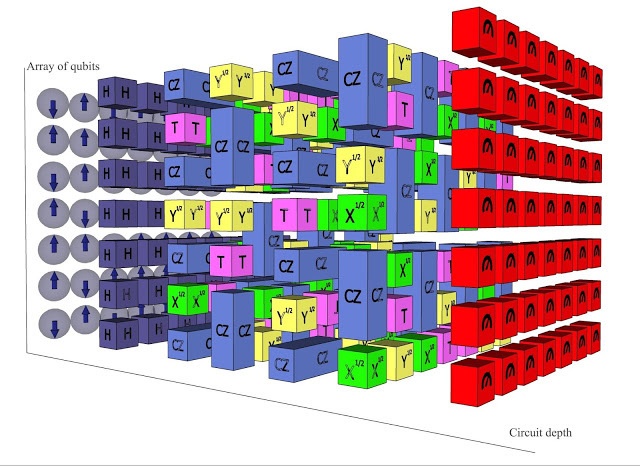
Ruimte-tijd-volume van een quantumcircuit-berekening. Bron: Google
:strip_icc():strip_exif()/i/2001777363.jpeg?f=fpa_thumb)
:strip_icc():strip_exif()/i/2001735019.jpeg?f=fpa_thumb)
/i/2007132430.png?f=fpa)
:strip_exif()/i/2003551924.jpeg?f=fpa)
/i/2003431888.png?f=fpa)
/i/2001777375.png?f=fpa)
/i/1240844012.png?f=fpa)
:strip_exif()/i/2001874933.jpeg?f=fpa)
:strip_exif()/i/2001760909.jpeg?f=fpa)
:strip_exif()/u/160250/crop684decfc73353.gif?f=community){kind=small}
/u/27299/hoofd.png?f=community){kind=small}
:strip_exif()/u/163648/crop5a04133bc3ce5_cropped.gif?f=community){kind=small}
:strip_icc():strip_exif()/u/84706/crop5f48f03c9fe53_cropped.jpeg?f=community){kind=small}
./u/212961/Alfred%2520Max%2520Headroom.png?f=community){kind=small}
:strip_icc():strip_exif()/u/541367/crop6679306ef1f8f_cropped.jpg?f=community){kind=small}
:strip_icc():strip_exif()/u/237526/crop5e05c1d265781_cropped.jpeg?f=community){kind=small}
