Spanjaarden vinden nieuw patroon in priemgetallen

Twee Madrileense onderzoekers hebben een vooralsnog onopgemerkt patroon in de distributie van priemgetallen weten bloot te leggen. De ontdekking zou onder meer zijn weerslag op cryptografische beveiliging kunnen hebben.

De twee onderzoekers, Bartolo Luque en Lucas Lacasa van de Spaanse Universidad Politécnica de Madrid, ontdekten een tot dusverre onbekende wetmatigheid in de distributie van priemgetallen. Op het eerste gezicht lijken priemgetallen - getallen die alleen door zichzelf en door 1 deelbaar zijn, willen ze een geheel getal als quotiënt opleveren - willekeurig voor te komen. Mede hierdoor is het zoeken naar grote priemgetallen, die onder meer in de cryptografie gebruikt worden, een rekenintensief karwei: het is niet mogelijk om een computer aan de hand van een formule in een reeks getallen de priemgetallen aan te laten wijzen.

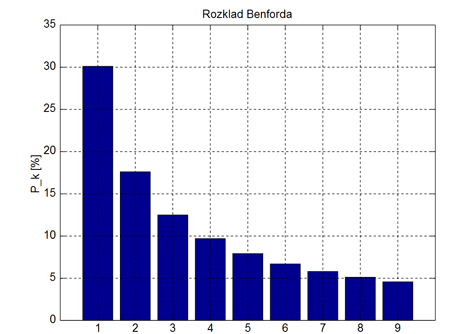
De twee Spaanse wiskundigen hebben ontdekt dat een verschijnsel dat als de Wet van Benford bekend staat, ook voor beperkte reeksen priemgetallen geldt. Deze wet stelt dat de verdeling van cijfers in willekeurige getalreeksen een logaritmische schaal volgt. Hoewel priemgetallen zich niet aan deze wet houden, lijken deelverzamelingen priemgetallen wel een generieke vorm van deze wet te volgen. Het duo ontdekte dat priemgetallen deze Generieke Wet van Benford volgen, waarbij het priemgetalstelling de verdeling van de eerste cijfers van de priemgetallen voorspelt. Bovendien hebben Luque en Lacasa vastgesteld dat de Riemann-hypothese, die voorspellingen over de verdeling van priemgetallen doet, zich eveneens aan de Generieke Wet van Benford houdt.

Het werk van de twee mathematici zou kunnen worden toegepast om verdelingen die niet aan de Wet van Benford voldoen met behulp van de Generieke Wet van Benford toch te structureren. Die generalisatie zou betekenen dat 'de' Wet van Benford slechts als een speciaal geval van de Generieke Wet van Benford gezien moet worden.

Het werk van de Spanjaarden zou de analyse van getalreeksen kunnen vereenvoudigen. Zo zouden bepaalde vormen van fraude, zoals het vervalsen van cijfers in een boekhouding, makkelijker bewezen kunnen worden: de 'natuurlijk ontstane' getalsverdeling in correcte boekhoudingen houdt zich normaliter aan de Wet van Benford, maar verdelingen van frauduleuze, dus verzonnen getallen niet.