Preview van nVidia's vertex shaders

In nieuwe lijn nVidia videochips die onder andere bestaat uit NV20, NV20A en NV25 zal nVidia de mogelijkheden van T&L flink uitbreiden. De huidige T&L methode is namelijk verre van ideaal, hij is inflexibel en heeft te weinig functies. Een van de dingen die daar verandering in moet brengen zijn de OpenGL extensies van NV_VERTEX_PROGRAM. Aangezien DirectX 8 en de laatste beta Detonator drivers al ondersteuning hebben voor deze features kon Reactor Critical er een interessant artikel over schrijven:

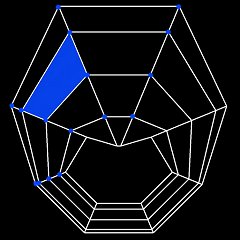
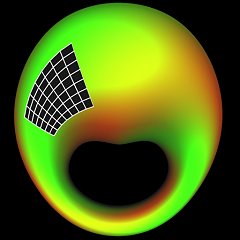
NVidia's watchword is "trimming down the extra levels of abstraction". What does the corporation have to offer to deliver on its promise? They have a solution: discarding the standard pipeline altogether and taking it into one's own hands to program the geometry processors. As a result, software engineers are required to master a specific RISC-oriented NV_VERTEX_PROGRAM assembly language. Be advised, however, that you need not rush to your computer to view the venerable company's Web site in your quest for a compiler for that language. NVidia would have had hell to pay to achieve compatibility with the major and popular development environments and existing 3D graphics APIs if it had followed that course. The compiler is going to be built right into future OpenGL drivers.[break]Met andere woorden: de programmeur kan volledige controle over de T&L van de videochip krijgen als hij bereid is de assembleertaal van de GPU te leren, die gelukkig maar uit 17 verschillende instructies bestaat. Een programma kan uit maximaal 128 instructies bestaan en dat is voldoende voor bijvoorbeeld een interpolatie van 16 matrices. Deze vertex programs (of vertex shaders, zoals ze ook wel genoemd worden) zijn ideaal voor programmeurs en driverschrijvers om extra features aan de kaart toe te voegen, zoals mist en high order surfaces:[/break] The idea behind the spline surface method is that a model without complex geometric details can be approximated through a set of flats. Figure 1 shows a wire model of a deformed torus; the same torus is in Figure 2, but it is covered by spline surfaces. One spline section remains unfilled. This section corresponds to the face colored in blue in the original model. Sixteen control points (also highlighted) are applied in forming the spline patch. The patches are constructed with the help of Bezier bicubic polynomials. If the values were calculated directly, an interpolation of the coordinates and the generation of the normals would require far too much even for an implementation using vertex programs. It is possible to reduce the number of calculations dramatically (down to about 5-6 machine instructions per vertex) by performing certain pre-processing. It is probable, though, that the new generation GPUs will be able to conduct a hardware rendering of curved surfaces (such as NURBS). Then it will be possible to deal with spline surfaces more efficiently.

Reacties (17)

[GarBaGe]

Als dit spul in de GF3 komt te zitten, heb ik in ieder geval een reden om mijn oude GF weg te doen.
Hardware NURBS samen met geheugenbandbreedte besparende HSR (wat ook op de V5 zit) maakt deze kaart wreed veel mooier en sneller dan mijn huidige GF.
Overstappen die hap

Voor de leken: NURBS zijn Non Uniform R... Bezier Splines (of zo iets). Dat betekent dat je mbv een aantal parameters dus volstrekt ronde curves kan maken. Dus niz meer benaderen met vlakjes of rechte lijnen, maar gewoon kromme lijnen. Niet alleen in 2D, ook in 3D. Perfecte bollingen enzo. Noem maar op. (dit is overigens ook te zien aan de plaatjes. Links de hoekige huidige versie, rechts de nieuwe NURBS. Het is gewoon echt veel beter )

[BurningSheep]

Non-Uniform Rational B-Splines

[Dr. Cheeks]

Wat niet wegneemt dat NURBS uiteindelijk voor het renderen gewoon benaderd worden door een getesseleerde mesh. Maar je kan er natuurlijk wel voor zorgen dat deze benadering dynamisch is. Dus veel vertexes in scherpe hoeken en net zoveel als nodig is om bij een zekere resolutie etc. een mooi 'ogenschijnlijk ronde' verschijning te krijgen. NURBS geven je zo veel meer flexibilitiet en kwaliteit dan statische meshes. Goede zaak dus

[Helox-in-a-box]

T&L units beginnen gwoon op CPUs te lijken, strax gaat Nvidia AMD en Intels ass kicken met hun nieuwe 64 bits NV40 voor de socket370 en kvraag me af of tie egt NURBS hardwarematig ondersteunt, ik kan nu ook gwoon met NURBS werken op mn G400 maar mn g400 heeft geen hardwarematige ondersteuning, het plaatje dat je ziet kan gwoon met 3dsmax of maya gemaakt zijn

[mth]

Kijk maar eens naar de vector units van de PS2, die zijn ook programmeerbaar. Op Ars Technica staat een mooi artikel daarover. Dit is natuurlijk iets heel anders dan een CPU: dit zijn gespecialiseerde processoren, heel krachtig voor een specifieke set taken en vrijwel nutteloos voor de rest.

[Chickendorp]

Wat is of zijn NURBS eigelijk?
Of is eht heel dom dat ik dat niet weet?

[Verwijderd]

NURBS.
www.webreference.com/3d/lesson35/
www.webreference.com/3d/lesson36/
www.webreference.com/3d/lesson37/
www.webreference.com/3d/lesson38/
www.webreference.com/3d/lesson39/

www.andromeda.com/people/ddyer/opengl.html

University of Manchester nurbs library:
ftp://unix.hensa.ac.uk/pub/misc/unix/nurbs/

[Erikie]

ow heerlijk..!! nu alleen nog hardwarematige refraction / reflection / radiosity / caustics, en we zitten in de matrix!

[Verwijderd]

Je vergeet hardware matige, real-time ray-tracing

[MPCX]

De NURBS mogen dan wel inderdaad parametrisch zijn,
ze worden in rendertijd gewoon als polygonal meshes gezien. Ik weet trouwens niet of het zo verstandig is om je geheel op "real-time" nurbs te gaan concentreren,daar komt een berg reken werk bij kijken daar word je niet goed van. subdivision surfaces (het smoothen van een mesh met behulp van bezier cureves) zijn qua gebruikte resources een stuk effectiever.

[DaBit]

Ehm, subdivision surfaces gebruiken geen Bezier curves hoor...

Subdivision surfaces gaan uit van een (relatief) lowres polygonal model, en subdividen deze adaptief naar hogere resoluties.

Wat jij bedoelt is waarschijnlijk adaptieve subdivisie van Bezier patches. Deze zie ik overigens nog wel eens ooit in HW komen, omdat als je je interpolators opgezet hebt, dan is het uitrekenen van nieuwe punten peanuts, en erg snel. Ongeveer 3-4x zoveel werk als bij een triangle.

[GA!S]

Gaat echt de goede kant op zo, ik hoop dat bijvoorbeeld Elsa zich (nu ze zich niet meer op het door-ontwikkelen van reference-boards richt) nu gaat concentreren om goede professionele drivers voor deze kaarten te maken. Stel je eens voor dat je inderdaad met deze GPU's vloeiend NURBS in je viewport kan renderen.
Als de hardware zo algemeen wordt komt de high-end markt wel een heel stuk dichter bij voor de thuisgebruiker. (was al met de Quadro )
Erg goede ontwikkelingen!

[X1pheR]

Vraagje, wat gaan die nieuwe NV20 bordjes, etc kosten? Het wachten waard of gewoon een Geforce2 GTS kopen?

Greetz...

[Verwijderd]

hmmm, als dr ee proc op zit, kan die met die instructies dan ook een paar koetjes grazen... zou hier een driver voor geprogd kunnen worden... Moooh

[MPCX]

ehm dat bedoeling dus.
ik was in de war met, inderdaad, patches.
er is echter ook een manier om meshes relatief te smoothen met controlpoints.
Bijv in MAX3.0 kun je een NURMS gooien boven op je mesh, wat dus een Non Uniform Rational Meshsmooth is. Waarmee je de hoeveelheid waarmee
er ge-smoothed wordt (wat een k*t woord) kunt controleren.Die kunnen als bezier-curve control points
gezien worden.
Nurbs zijn btw nog niet echt uit ontwikkeld, dus patches zijn veel effectiever.
dus.

[Killemov]

Oh Man! NURBS in hardware! Yes!

[speedwell]

VET STOER