Turing-machine: de grenzen van berekenbaarheid

De praktijk

Dat de methoden om berekenbaarheid te bepalen Turing-equivalent zijn, wil natuurlijk nog niet zeggen dat alle talen en systemen even snel zijn: deze theoretische complexiteitsmodellen zijn niet zomaar naar de praktijk te vertalen. Cobham's these stelt wel dat alleen problemen in P in redelijke tijd kunnen worden opgelost, maar ook polynomiale tijd kan heel lang duren.

Zo zegt het tijd-hiërarchie-theorema dat P bestaat uit een hiërarchie van problemen die steeds moeilijker op te lossen zijn. Dat wil zeggen dat een DTM steeds meer tijd nodig heeft om het antwoord uit te rekenen, bijvoorbeeld omdat de verwerkingstijd kwadratisch in plaats van lineair is ten opzichte van de lengte van de inputstring. De consequentie daarvan is dat er ook P-problemen zijn die oneindig veel polynomiale tijd kosten om op te lossen. Hetzelfde geldt voor de structuur van NP.

Het ruimte-hiërarchie theorema zegt iets vergelijkbaars voor de beschikbare geheugenruimte (de tape): je kunt steeds complexere problemen oplossen naarmate je meer geheugenruimte tot je beschikking hebt. Dat is uitermate relevant als je bedenkt dat de beschikbaarheid van een oneindig lange tape het belangrijkste onderscheid is tussen een Turing-machine en een echte computer.

Aan de andere kant zijn er een heleboel algoritmen bekend die misschien niet de exacte oplossing van een niet-polynomiaal probleem geven, maar wel een goede benadering kunnen leveren.

Parallelle systemen

De complexiteitshiërarchie van P en NP is maar het topje van de ijsberg. De theoretici hebben deze structuren uitgebreid met allerlei nieuwe problemen en klassen. Met de opkomst van multicoreprocessors en quantum computing zijn met name Nick's Class en BQP in de belangstelling komen te staan.

Nick's Class bevat alle problemen die met een parallelle Turing-machine in polylogaritmische tijd zijn op te lossen, dat wil zeggen: sneller dan polynomiaal. Zo'n parallel systeem bestaat uit een beperkt aantal rekeneenheden rond een gedeeld geheugen. Omdat een DTM een parallel random access machine kan simuleren, vallen de problemen in NC ook in P. Tegelijkertijd is het vermoeden dat er ook problemen zijn die geen voordeel hebben bij meerdere rekeneenheden, en dus inherent sequentieel zijn. Die klasse van problemen die wel in P vallen maar niet in NC, heet P-Compleet.

Dit theoretische concept zien we terug in de softwarewereld, waar de Wet van Amdahl een relatie legt tussen de parallelliseerbaarheid van een algoritme en de maximale versnelling die kan worden verkregen op een parallelle computer.

Quantum computers

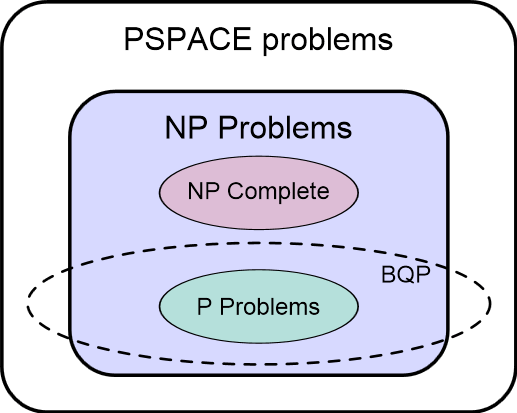
BQP, kort voor Bounded Error Quantum Polynomial, bevat de problemen die, in elk geval hoogstwaarschijnlijk, in polynomiale tijd op een quantum-Turing-machine zijn op te lossen. Daarbij moet het aantal quantum bits weer polynomiaal beperkt zijn ten opzichte van de input string. De BQP-klasse omvat wel P, maar niet NP-Compleet. Dat betekent dat een quantumcomputer niet fundamenteel krachtiger is dan een traditionele computer, en alleen sneller is voor bepaalde NP-Intermediate problemen. Maar onbeslisbare problemen blijven onbeslisbaar, en NP-Complete problemen blijven niet-polynomiaal.



Helaas voor de veiligheidsleveranciers valt het algoritme van Shor binnen de klasse BQP. Dat wil zeggen dat er een quantumalgoritme bestaat waarmee de priemfactoren van getallen kunnen worden gevonden. Het in priemfactoren ontbinden van getallen is een NP-probleem, en de moeilijkheid daarvan is de basis van de public-keycryptografie die we dagelijks op het internet gebruiken. Dat betekent dat we op termijn nieuwe algoritmen moeten inzetten die informatie-theoretisch veilig zijn.

Reacties (51)

Leuk artikel en wel duidelijk, alleen was het misschien ook leuk in de intro de mindere kanten te vertellen over wat turing is aangedaan;

In 52 heeft de britste staat hem aangeklaagd voor homoseksualiteit en gaf hem een keuze; chemische castratie of een levenslange gevangenisstraf, hiervoor is geen excuus gebracht tot 2010 - en zelfs in dit excuus heeft de britste staat niet officieel gemeld dat het excuus over de chemische castratie ging.

Ook wouden de Britten de al Turings uitvindingen(het kraken van de enigma code, etc) niet onder turing's eigen naam laten vallen maar onder de naam van de staat - Dit omdat hun vonden dat een homoseksueel geen wetenschaplijk genie kon zijn.

voor de rest, prima en mooi artikel. Wonderbaarlijk man die Turing.

U vraagt...

http://www.bbc.co.uk/news/science-environment-18561092

Dit weekend is daar blijkbaar uitgebreid over gesproken... er wordt nu zelfs openlijk aan zijn zelfmoord getwijfeld... alhoewel het een 'ongeluk' wordt genoemd.

Turing is inderdaad schandalig behandeld, maar over zijn zelfmoord schijnen toch twijfels te bestaan.

nvm, dubbel

[Reactie gewijzigd door blobber op 23 juni 2012 12:39]

P en NP zijn niet de enige klassen (bijv. EXPTIME wordt vergeten, waarin problemen zitten die zeker moeilijker zijn dan de problemen in P en NP), dus in het P = NP? deel moet e.e.a. herschreven worden.

Bovendien is het jammer dat de schrijver al aanneemt dat P != NP, bijvoorbeeld in deze zin:

"Deze Niet-deterministisch Polynomiale problemen zijn alleen op te lossen met algoritmen waarvan de rekentijd sneller dan polynomiaal toeneemt als de invoerstring langer wordt."

Dat is natuurlijk alleen waar onder aanname dat P != NP, maar die aanname staat nergens vermeld.

Niemand beweert dat NP-compleet de klasse met moeilijkste problemen is. Ik zie niet wat er mis is met het stukje P =? NP, want het is een heel terechte vraag die meer te maken heeft met Turing-machines dan de klassen EXPTIME of NP-hard.

Die aanname P != NP is heel logisch en staat wél in het artikel:

De vraag of uiteindelijk voor alle problemen in de klasse NP een polynomiaal algoritme kan worden gevonden, waarmee die problemen dus in de klasse P terecht komen, wordt door de theoretici P =? NP genoemd. Het vermoeden is echter dat er problemen zijn waarvoor helemaal geen P-algoritme kan bestaan, maar dat bewijzen is vers twee. Dit is niet voor niets een van de zeven Millennium-vraagstukken, waar een geldprijs van een miljoen dollar aan is verbonden.

Bovendien lijken er problemen te zijn die wel in NP zitten maar niet in P of NP-Compleet.

in dat stukje van het artikel staat letterlijk dat - aangenomen dat P != NP - niet-P problemen dientengevolge in NP zitten, totale onzin dus.

overigens, het stukje wat jij quote is een mooi voorbeeld van nog een foute formulering door onzorgvuldigheid:

"Het vermoeden is echter dat er problemen zijn waarvoor helemaal geen P-algoritme kan bestaan." Wat bedoeld wordt: "Het vermoeden is echter dat er problemen in klasse NP zijn waarvoor helemaal geen P-algoritme kan bestaan"

Als je wetenschappelijk bezig wil wezen, moet je wel precies te werk gaan (mathematical rigor).

@Garma, de formulering zoals ie er nu staat kun je niet uitleggen als kloppend, zonder P != NP aan te nemen. Je draait de zaak juist om, je zegt dat omdat er nog niet zo'n algoritme gevonden is, dat P dus niet gelijk is aan NP. De quote "Deze Niet-deterministisch Polynomiale problemen zijn alleen op te lossen met algoritmen waarvan de rekentijd sneller dan polynomiaal toeneemt als de invoerstring langer wordt." is _juist_ de essentie van P = NP? vraag.

[Reactie gewijzigd door justinkb op 23 juni 2012 19:58]

Je kunt de formulering wel uitleggen als kloppend met een beetje goede wil:

"Deze Niet-deterministisch Polynomiale problemen zijn (op dit moment) alleen op te lossen met algoritmen waarvan de rekentijd sneller dan polynomiaal toeneemt als de invoerstring langer wordt."

"Deze Niet-deterministisch Polynomiale problemen zijn alleen op te lossen met algoritmen waarvan de rekentijd sneller dan polynomiaal toeneemt als de invoerstring langer wordt."

Dat is natuurlijk alleen waar onder aanname dat P != NP, maar die aanname staat nergens vermeld.

volgens mij klopt het artikel strikt genomen wel, want zolang er geen bewijs is voor P = NP dan is er dus geen algoritme dat NP problemen sneller oplost. Het zou kunnen dat er wel een algoritme is, maar dat is op dit moment in elk geval niet bekend. P =? NP gaat over de vraag of dat algoritme uberhaupt bestaat.

Leuk om een verhaal over complexiteit te zien op Tweakers! Het is inderdaad een erg nuttige theorie om ingewikkelde praktische problemen te bestuderen. De opgedane kennis kun je vervolgens gebruiken in het ontwerp van je oplossingsmethoden. Veel roosterings- en planningsproblemen uit de praktijk zijn NP-hard. Vaak hebben dit soort problemen wel weer deelproblemen die wel efficient op te lossen zijn. Soms kun je de oplossing van een makkelijk deelprobleem gebruiken om iets nuttigs te zeggen over de best mogelijke oplossing voor het moeilijke probleem.

Wat mij betreft is er op dat gebied ook een keerzijde aan de theorie van NP-volledigheid: zodra bekend is dat een probleem "lastig" is geven mensen het al snel op om goede oplossingsmethoden te verzinnen. Toch geldt vaak voor veel praktische problemen dat je een heel eind kunt komen. Zo zijn er voor het genoemde handelsreizigersprobleem programma's die instanties met een paar honderd steden in een seconde kunnen oplossen (en staat het wereldrecord op 85900 steden voor het ontwerp van een chip). Over deze ontwikkeling is vorig jaar nog een voor leken geschikt boek, "In pursuit of the traveling salesman" uitgekomen, wat zeker een aanrader is.

Voor tweakers die de complexiteitstheorie an sich interessant vinden is er vorig jaar ook nog een enorm boek uitgekomen dat deze onderwerpen op een wat speelse, maar veel diepgaandere manier uitlegt: "The nature of computation".

Nog een lichtvoetiger aanvulling: vorige week is de film "Travelling Salesman" in premiere gegaan. Daarin wordt uitgewerkt wat er zou gebeuren als P=NP.

Site film:
http://www.travellingsalesmanmovie.com/

Leuk om iets over complexiteitstheorie te zien. De vraag P=NP is trouwens minder belangrijk dan we misschien denken, R.J. Lipton heeft daar een leuk stuk over geschreven: http://rjlipton.wordpress...pnp-an-ill-posed-problem/

Daar staat ook een goede quote in van Alan Perlis:

For every polynomial algorithm you have, I have an exponential algorithm that I would rather run.

Leuk fimpje, behalve dat het compleet niet laat zien hoe 2+2 uitgerekend wordt door de machine (misschien was dat ook een beetje teveel verwacht).

Probleem is dat'ie daar vijf minuten over doet Maar voor wat extra uitleg over de werking, zie http://www.legoturingmachine.org/, daar staan ook links naar de implementatie van het optelprogramma e.d.

Als je echt pech hebt komt er 3 uit

"Het in priemfactoren ontbinden van getallen is een NP-probleem"

Het ontbinden in factoren van een getal is puur een P-probleem, met zelfs een bijzonder eenvoudig algoritme. Pas als je niet het getal zelf maar de lengte van het getal als invoerparameter neemt (dus de logaritme van het getal i.p.v. het getal zelf) dan introduceer je daarmee automatisch (logaritme <-> exponentieel) een exponentieel verloop, en dus NP.

Het ontbinden van een getal in zijn priemgetallen is niet(deterministisch) polynomiaal. Het testen dat de oplossingen correct is polynomiaal. Dus het ontbinden van een getal in zijn priemfactoren is wel degelijk NP. Ik snap dan ook niet wat dat dan te maken heeft met de "de lengte van het getal als invoerparameter"...

Mocht je gelijk hebben, dan heb je een bewijs gegeven dat P=NP. En dat lijkt me een beetje sterk en zullen een aantal jongens in o.a. de cripto-wereld erg nerveus worden.

Edit: toevoeging tweede alinea.

[Reactie gewijzigd door FSVZ op 23 juni 2012 12:05]

Je bedoelt: er is geen polynomiale-tijd algoritme bekend voor priemontbinding. Of het probleem van priemontbinding wel of niet in P zit, weten we niet. Je hebt verder helemaal gelijk.

Wat Ettepet zegt is: als je de tijdscomplexiteit uitdrukt in termen van de invoer zelf, in plaats van de bitlengte van de invoer, dan is de complexiteit lager en zit priemontbinding in P. Dat is onzin, omdat dat niet de definitie van P is.

[Reactie gewijzigd door z.jeroen op 23 juni 2012 23:05]

Heb hier net een examen over gehad. Best wel interessant en vrij goed uitgelegd zodat een iets of wat meer leek dat ook wel kan verstaan.

Maar ik snap nog niet helemaal om wat voor een soort problemen hier hier gaat. Gaan deze theorieën over wiskundige problemen, zoals differentiaal vergelijkingen. Want ik kan mij niet voorstellen dat je een ander soort probleem op zo'n Turning tape kan formuleren.

[Reactie gewijzigd door kwinvdv op 24 juni 2012 01:53]

Formeel gaat het om problemen met een ja/nee-antwoord, zogenaamde decision problems. Bijvoorbeeld: is x een priemgetal? Maar het kan ook zijn: is f een oplossing van de differentiaalvergelijking x? of: heeft de vergelijking x een oplossing?

[Reactie gewijzigd door z.jeroen op 23 juni 2012 22:50]

"Maar ik nog niet helemaal om wat voor een soort problemen hier hier gaat."
Allerlei soorten problemen, van het vinden een kortste pad in een graaf tot het decoderen van berichten.

"Gaan deze theorieën over wiskundige problemen, zoals differentiaal vergelijkingen."
Nee, de turing theorien, om het maar zo op te noemen, worden vaak gebruikt om problemen te classificeren.

"Want ik kan mij niet voorstellen dat je een anders soort probleem op zo'n Turning tape kan formuleren."
Ja dat is mogelijk, want elk probleem kan je zo formuleren dat er een Turning Machine er voor kan worden gemaakt.

Een kleine toevoeging: Voor de zogenaamde onbeslisbare problemen geld dus dat er juist geen TM voor gemaakt kan worden. Het halting probleem beschreven in het artikel is hier een voorbeeld van.

Duidelijk verhaal. Ik had het idee dat een turing-machine de turing-test kon doorstaan, maar het gaat dus over 2 compleet verschillende dingen. Alleen de naam heeft nogal een grote overeenkomst.

De turingtest gaat over hoe goed een computer een mens na kan doen, terwijl de turing machine gaat over wat de computer kan.

Geeft maar weer aan met hoeveel gebieden Turing zich bezig hield. Naast KI en Informatica deed hij namelijk ook nog aan oa encryptie en biologie.

De turingtest gaat over de intelligentie van een systeem, niet perse het nadoen van een mens.

Ik vraag me af of jullie het wel gelezen hebben.

Een computer gaat door de Turing test succesvol wanneer het een mens heeft weten te overtuigen dat het zelf ook een mens is. Intelligentie heeft hier niks mee te maken, dit is Weak AI. Een computer dat daadwerkelijk intelligent is noem je een Strong AI.

Alan heeft met zoveel gebieden bezig gehouden omdat hij initieel bezig hield met KI, maar om KI te maken had hij een machine nodig die dat kon doen. Hiervoor had een machine nodig die dat kon doen, hij is toen een (theoritische) computer gaan ontwikkelen die dit kon. Dit is uiteindelijk de Turing machine geworden.

http://en.wikipedia.org/wiki/Turing_test
http://en.wikipedia.org/wiki/Strong_AI_vs._weak_AI
http://en.wikipedia.org/w...achinery_and_Intelligence

[Reactie gewijzigd door Anoniem: 249623 op 24 juni 2012 13:05]

De term 'KI' is in Nederland eigenlijk al geclaimd voor iets anders... hou het maar bij AI

Wat dan; Kunstmatige Inseminatie, kadastraal Inkomen ?
KI is volgens mij een prima gebezigde term in NL voor AI hoor ...

Offtopic: KI = Kadastraal Inkomen...

Complexiteitstheorie op tweakers? Talk about surprises... Dit soort materiaal zou ik wel vaker willen zien

idd, erg cool om dat hier tegen te komen.

True, hoewel het wel nog allemaal vrij basis is.

Tuurlijk, kattenpis dit! Ik begreep het meteen!