OGR-24 project geëindigd: DPC overtuigend op #1

Begin deze maand heeft distributed.net het einde aangekondigd van haar project OGR-24. Bij dit distributed-computingproject werd gezocht naar de OGR van 24 merktekens, die nu gevonden is. De Dutch Power Cows (DPC) hebben dit project winnend afgesloten; zij hebben de afgelopen jaren veruit de meeste OGR's onderzocht en eindigden daardoor ruimschoots bovenaan de teamranglijst.

Over OGR

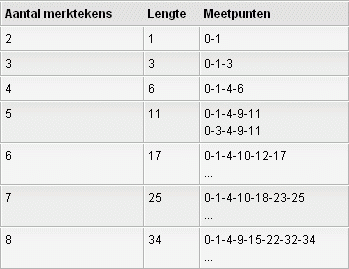
OGR staat voor Optimal Golomb Ruler. Eenvoudiger gezegd is het de kortst mogelijke liniaal met een bepaald aantal punten, waarbij alle maatstrepen op verschillende afstand van elkaar zitten. OGR's maken het mogelijk zo veel mogelijk afstanden te meten met een minimum aan meetpunten. Zo is het bijvoorbeeld mogelijk om met een OGR die vijf meetpunten omvat, tien afstanden te meten:

Juist de eigenschap dat met zo min mogelijk meetpunten zo veel mogelijk afstanden gemeten kunnen worden, maken OGR's interessant voor toepassing in bijvoorbeeld radiotechnologie, sensorplaatsing en röntgenapparatuur.

Het project

Er zijn in het verleden al veel mogelijke OGR's opgeschreven. Mogelijke OGR's, omdat er slechts van een beperkt aantal is aangetoond dat het ook werkelijk OGR's zijn. Het bewijzen van een OGR gebeurt door alle andere mogelijke linialen na te gaan, en te kijken of het een OGR is. Tot en met vier merktekens zijn OGR's nog redelijk goed uit het hoofd te bepalen, tot en met acht merktekens is het met pen en papier te doen.

Later bewezen de eerste computers hun nut; in 1972 al werden met behulp van een computer OGR's met negen tot en met elf merktekens bewezen. Tussen 1979 en 1994 werden OGR's van twaalf tot en met negentien merktekens bewezen, door steeds verder verbeterde computerprogramma's, maar daarna bleef het een tijdje stil. De exponentiële toename in te doorzoeken mogelijkheden zorgde ervoor dat het niet langer handig was om OGR's met slechts één computer te zoeken. In 1997 werden er clients ontwikkeld waarmee het werk te verdelen valt over meerdere computers. OGR-20 tot en met OGR-23 werden hiermee bewezen. In 1999 werd het overleg met distributed.net gestart om OGR's op wereldwijde schaal te gaan zoeken. Half 2000 werd hiervoor de eerste distributed computing-client voor OGR-24 uitgebracht.

DPC en OGR

OGR werd aangekondigd als project op het moment dat DPC druk in gevecht was met Team AnandTech bij RC5-64, het eerste project waar DPC aan meedeed en waarmee DPC zijn wereldwijde DC-bekendheid heeft verworven. Er was op dat moment nog maar weinig interesse in OGR. Nadat AnandTech was verslagen en de voorsprong groeide, werd OGR populairder. Ook hier werden nu de pijlen op de #1 gericht. OGR was inmiddels echter een gebundeld project van OGR-24 en OGR-25, waarbij de eerste fase van OGR-24 eigenlijk al grotendeels voorbij was toen DPC goed op gang kwam. De #1 bij OGR-25 werd dan ook eerder bereikt dan bij OGR-24. Dat gebeurde pas toen wat resten OGR-24 beschikbaar kwamen en DPC er vol op dook.

Bij de tweede fase van OGR, waarbij de vele zeer kleine porties gecombineerd konden worden om de infrastructuur niet in gevaar te brengen, liet DPC wederom zien zeer snel over te kunnen schakelen naar nieuwe clients en bouwde de voorsprong nog verder uit.

Einde van het project OGR-24

Ruim vier jaar na de start van het project is de kortste liniaal uiteindelijk bepaald. Het is:
24/9-24-4-1-59-25-7-11-2-10-39-14-3-44-26-8-40-6-21-15-16-19-22

Deze kortste liniaal is als eerste gevonden door Matt Richards (Matt_R in #distributed) op 24 mei 2004. Mitsuru Aoki van het SEGA Users Group Team bevestigde dit op 3 juli 2004. Maar pas toen Sebastian "Pax" Schmitz op 13 oktober 2004 de allerlaatste mogelijkheid had ingeleverd was duidelijk dat het echt de kortste OGR-24 was.

De liniaal is dezelfde als die in 1967 werd voorspeld. Hiermee is OGR-24 ten einde en kan in de lijst worden vermeld dat OGR-24 bewezen is. DPC mag zich met recht de grootste deelnemer noemen. Namens DPC en ook namens distributed.net worden alle deelnemers bedankt voor hun deelname.

Voortgang van het project OGR

Het OGR-25 project loopt nog volop. DPC heeft hier twee weken terug zelfs de 500 miljoen mijlpaal gehaald. De verwachting is dat de algoritmes om OGR's te bewijzen de komende jaren nog behoorlijk verbeteren, zodat na het afronden van OGR-25 een OGR-26 verwacht kan worden. Wie dit een interessant project vindt, kan in het vorige nieuwsbericht over OGR lezen hoe er kan worden meegedaan aan OGR-25.