Scholieren berekenen meest magische vierkant

Drie tieners uit Nijmegen hebben de internationale wetenschap versteld doen staan door een eeuwenoud wiskundig raadsel op te lossen. De scholieren wisten het meest magische vierkant ooit te construeren, stellen wiskundigen van de Radboud Universiteit in Nijmegen.

Een magisch vierkant, of tovervierkant, is op zo'n manier gevuld met getallen dat de kolommen, rijen, diagonalen en zelfs cirkelvormen opgeteld elk dezelfde uitkomst geven. De Amerikaanse wetenschapper Benjamin Franklin wist 250 jaar geleden vijf speciale supermagische vierkanten te fabriceren, maar de wetenschap kon er niet achter komen hoe hij dit voor elkaar kreeg. De Nijmeegse wiskundige Arno van den Essen presenteerde vorig jaar al een elegante oplossing voor het Franklin-mysterie. De prestatie van de zeventienjarige Jesse Hoekstra en Willem Schilte van het Dominicus College in Nijmegen en hun vijftienjarige vriendin Petra Alkema, is volgens hem echter ongekend. Zij zijn er eind vorig jaar tijdens een masterclass in geslaagd een Franklin-vierkant van twaalf bij twaalf hokjes te vullen. 'De ultieme uitdaging', volgens hoogleraar Nico Landsman van de Radboud Universiteit Nijmegen.

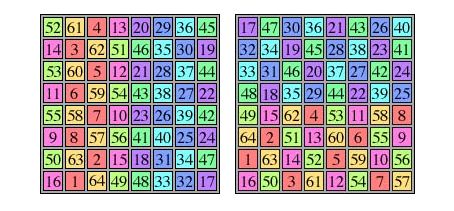
Het vierkant bestaat uit 144 hokjes met de getallen 1 tot 144, waarbij de som van elke rij en elke kolom 870 is. Maar dat niet alleen, ontdekte Arno van den Essen. Een bijzondere eigenschap van de getallenverzameling is dat het ‘eenderde Franklin magisch’ is, wat inhoudt dat de som van elk derde deel van een rij en elk derde deel van een kolom gelijk is aan 290. Verder is het vierkant ‘panmagisch’: alle diagonalen en parallelle gebroken diagonalen hebben als som 870. Scholier Jesse: 'We hebben het vierkant verzonnen door een beetje te puzzelen en het in kleinere vierkantjes op te delen. We kwamen er pas later achter dat er bijzondere dingen inzaten, zoals gespiegelde figuren.'

Reacties (127)

[Chrono Trigger]

Toeval, of werpt de huidige en slechtgeroemde vorm van onderwijs toch zijn vruchten af?

[Anoniem: 202609]

even ter informatie wat master class is, ik volg het zelf ook en bij ons is het uit je hoofd (dus zonder grafische of andere rekenmachine) vergelijkingen op te lossen. althans dat is het op het saxion te enschede. ik zelf vind het leuk en het is goed te doen, heb er alleen te weinig tijd voor...

maar wat mijn punt is die "master class" is dus in feite geen slechtgeroemde vorm van wiskunde maar juist de wiskunde die iedereen hoort te krijgen

edit:

@therat10430
ik doe zelf havo 4 en ben 17 jaar, master class is bij ons iets om ons wat meer met het hoofd te laten doen nu we nog jong zijn (het word in dit gevalg georganiseerd door het saxion) (het is puur vrijwillig) als je een hogere wiskunde dan wiksunde B2 zou bedenken komt het denk ik in de buurt met wat ik als master class opvat...

(en ja, Saxion =HBO)

[roy-t]

Een masterclass is toch een algemeen begrip, en niet iets wiskunde specifieks? Ook gaat het hier om jeugdigen van 17 en 15jr, ik denk niet dat die dezelfde les krijgen op de middelbare school als jij op het Saxion (=HBO?)

[TheMazzter]

Met masterclass kan hier ook een soort van curses/introductie voor 5/6 VWO'ers bedoeld worden. Die bestaan dan uit een of meer middagen op een universiteit iets doen met andere 5/6 VWO'ers onder begeleiding van een aantal docenten/studenten van de universiteit. In dit geval dan waarschijnlijk een masterclass voor wiskunde.

[Quacka]

hoe lager het niveau, hoe slechter het onderwijs.

Gemiddeld gezien zijn vwo-leerlingen bijv veel serieuzer met hun studie bezig, dan vmbo-leerlingen.
Het huidige nederlandse systeem gaat uit van eigen initiatief, van zelfdiscipline etc etc.
Geschikt dus voor mensen zoals hierboven in het stuk genoemd.

Maar vmbo-ers hebben dat veel minder. En als ik naar mezelf kijken als oud-havoleerling: ik had toen echt niet zoveel zelfdiscipline. Had ik nu op school gezeten, dan had ik wellicht minder geleerd.

We moeten dus mensen die het aan kunnen veel vrijheid geven en de groep die dit niet kan niet teveel vrijheid geven. Bak dat maar eens in een werkend systeem... (heb je de oplossing, dan kan je solliciteren bij het ministerie van onderwijs)

[SED]

Beetje onzinnige opmerking en vergelijking.

Het onderwijs bij de meeste VMBO shcolen is prima en toegerust voor wat een VMBO er moet leren en kennen en beheersen. Dat het jou nu niet aan zou spreken zegt weinig tot niets over wat je nodig hebt om in deze tijd een opleiding te volgen.
Het "nieuwe leren" is veel minder omstreden dan de meesten denken of de indruk die bepaalde reactionaire groepen willen wekken.
Alleen kennis opdoen is niet meer van deze tijd . Dat sommige scholen daarin wat doordraaien heeft meer te maken met zaken zoals subsidies en stimulans om samen met commerciele partners zo te werken.

Het feit dat jij nu je kennis verdiept via een site als tweakers zegt eigenlijk al genoeg over hoe jij beter had kunnen leren als je naast kennis ook extra aandacht voor vaardigheden en compententies gekregen had.

[Anoniem: 96271]

...of de populariteit van Sudoku...

[Anoniem: 17190]

We kwamen er pas later achter dat er bijzondere dingen inzaten, zoals gespiegelde figuren.'

toeval dus

[mad_max234]

Van die gespiegelde figuren ja, de rest hard denk werk.

[Crack]

Elk magisch vierkant heeft toch spiegelingen?
Tegenover de laagste waarde ligt de hoogste. Tegenover de 2e waarde de maximale min 1, etc.

Bij oneven magische vierkanten ligt de middelste waarde ook altijd op de kruising van de diagonalen, omdat voor gelijke totalen die waarde op beide diagonalen moet voorkomen.

Dit moet je niet met brute force proberen op te lossen. Met een beetje inzicht kan je enorm veel mogelijkheden uitschakelen. Kijk eens naar de code van: http://magie.nl.eu.org/magicsource.html .

[elmuerte]

2 van de X duizend is niet iets om zigge conclusies uit te halen, of uberhaupt om trost op te zijn.

[Anoniem: 176826]

Zeg het waren wel drie leerlingen. Het artikel hierboven is wat dat betreft nogal slecht geschreven, maar het magische 12*12 vierkant is opgesteld door:
Jesse Hoekstra, Willem Schilte en Petra Alkema.

Het is dat ik dit bericht elders ook al had gelezen, anders was ik er in dit artikel ook finaal aan voorbij gegaan.
Je hebt gelijk, drie leerlingen van die zoveel duizenden is niet bepaald representatief.

Hun begeleider gaf zelf ook aan dat hij heel verbaasd was dat het ze was gelukt en dat hij vooral onder de indruk was van hun doorzettingsvermogen.
Zoals ze zelf ook al aangaven, is het vooral een stukje puzzelen en moet je er vooral veel tijd in steken.

(Ik ben wel eens begonnen aan een kleinere variant en ze zijn echt niet eenvoudig, dus zeker petje af voor deze drie vijftienjarigen.)

[IntToStr]

Volgens het stuk in de krant hebben ze het probleem opgedeeld in kleinere vierkanten. Een aantal eigenschappen die door hun methode ook werden bereikt, werd door de leerlinge als "toeval, wisten we niet eens" afgedaan. Bijv. die 1/3 regel. Dit zat volgens mij gewoon in hun systeem: namelijk 9 vakjes van 4 bij 4 invullen.

Zonder die cirkels en doorlopende diagonalen is het heel eenvoudig om zoiets op te lossen voor 4x4 vakjes. Dan is het dus een kwestie van puzzelen...

Het zou best kunnen dat een computerprogramma start met een initieel vierkant dat nog niet alle eigenschappen heeft gaat rekenen en dan door een oplossingsboom gaat lopen, maar met de hand kun je misschien beter zoeken.

Het zal wel een combinatie van geluk en een systeem gemaakt door de persoon van de uni die ze had uitgedaagd dit te doen zijn geweest, maar niettemin, knappe prestatie!

Wij programmeurs kunnen dus nog niet voor alles zorgen

Edit: zie hieronder wat ik dus bedoelde met dat het heel eenvoudig is om een "standaard magisch vierkant" te maken. De problemen komen dan alleen bij die cirkels en doorlopende diagonalen...

[Ghost(NL)]

Ik vind het leuk voor ze, maar mij ontgaat het speciale aan dit vierkant. Mijn inziens kan een computer dit redelijk eenvoudig zelf berekenen en dus lijkt het mij niet zo'n extreem probleem lijkt mij het niet, beetje brute force er tegen aan en dan kom je een heel eind lijkt me.

Reactie op hieronder:

Brute force mag inteligent zijn hoor dus zoals onder jouw ook aangehaald, zodra iets niet klopt stoppen. Dat scheelt een behoorlijke factor aan tijd. Oh en kijk eens naar die link onder je, deze: http://magie.nl.eu.org/generator.html zo spannend is het dus niet, dus nogmaals ik mis waarschijnlijk iets.

[Zyppora]

Brute-forcen lijkt me een beetje sterk. Je hebt 144 verschillende vakjes/getallen, dus een totaal van 144! = 5,55 * 10²⁴⁹ verschillende mogelijkheden. Op een dualcore van 3 GHz cost je dat 2,93 * 10²³² jaar (ervan uitgaande dat je elke clockcycle een mogelijkheid per core kunt genereren en valideren).

Da's dus iets meer dan die 300 jaar.

Ziet er allemaal nogal astronomisch uit ... kan goed zijn dat ik ergens een denk/reken-fout maak ... of er een factor 10¹⁰⁰ naast zit ...

Edit: en dan nog niet te spreken over dat vierkant van 16 bij 16 vakken: 256! mogelijkheden
* Zyppora heeft respect voor deze wandelende wiskundeknobbels

@PiepPiep & MetalStef:

Volgens mij lezen jullie hier overheen:
"ervan uitgaande dat je elke clockcycle een mogelijkheid per core kunt genereren en valideren"

Het halverwege stoppen en met de volgende mogelijkheid verdergaan levert in dit theoretische geval dus GEEN tijdswinst op.

@GhostRider:

Ik denk dat wanneer een brute force intelligent wordt, je dan meer in de richting van een algoritme moet gaan denken, maar correct me if I'm wrong. Daarnaast zul je toch moeten bepalen of een (deel van een) mogelijkheid 'levensvatbaar' is voor de titel 'magisch'. Dacht je dat dat geen clockcycles kost? En zoals verderop al aangegeven: de link die je aanhaalt doet het met rijen en kolommen (en mogelijk ook diagonalen), maar niet met de overige requirements (cirkels, halve diagonalen, weet ik waar de oplossing allemaal aan moet voldoen).

[PiepPiep]

Wat je hier vergeet is dat een klein vierkantje van 2 bij 2 ook al een bepaald totaal moet hebben, zodra dat vierkantje al niet meer klopt ga je natuurlijk niet meer verder rekenen.

[Zyppora]

De vraag is of je het dan nog wel 'brute force' kan noemen Het is heel goed mogelijk dat een 'brute force' proces bij zijn derde poging (van de 5,55 * 10²⁴⁹) al DE oplossing heeft gevonden, dan kost het hem nog geen seconde. Maar ALLE mogelijkheden doorzoeken, zoals hierboven gesuggereerd wordt, is niet mogelijk: zolang bestaat het universum nog niet, en zolang zal het universum niet bestaan (want, dacht ik op wiki gelezen te hebben, protonen vervallen na 10⁶⁰ jaren).
[/rantmodus]

[Anoniem: 71510]

helaas bestaan er geen magische vierkanten van 2x2

[Gepetto]

1 1
1 1



Ik ken er zelfs eentje van 1x1

[iain]

helaas is dat niet mogelijk, want getallen mogen niet dubbel voorkomen
1x1 kan wel, maar is weinig wiskundig...

[MetalStef]

Onzin: Als je 144 vakjes wilt vullen, en die tel je allemaal bij elkaar op, komt het totaal van alle vakjes op 10440. Dat deel je door 12 (aantal rijen of kolommen) en daar komt dan 870 uit. Dus ongeacht hoe je het ding in weet te vullen, je weet al wat de uitkomst van elke rij moet zijn.

Dat betekent dat je na het invullen van de eerste rij al kunt bepalen of je een magisch vierkant aan het maken bent: Als de optelsom van de eerste rij geen 870 is, kun je opnieuw beginnen. Als je een dergelijke controle inbouwt, gaat je dat een grooooot aantal jaren rekenwerk schelen op je dualcore.

Edit: Dus dat wat PiepPiep zegt, maar dan ingewikkeld...

[Anoniem: 96271]

Het schijnt te werken met iets wat een 'algorithme' heet, zelf geloof ik daar niet zo in. Gewoon oneindig lang alle mogelijke combinaties proberen!

[powerflux]

http://magie.nl.eu.org/generator.html

t kan dus gewoon in no-time. (snap zelf niet hoe)

[diederik77]

@powerflux
maar daar zitten waarschijnlijk geen cirkelvormen in.

Ik begrijp alleen niet hoe ze dat willen gaan definiëren, met hokjes een cirkelvorm :-S
Je kunt hoogstens iets nemen wat er een beetje op lijkt

[Anoniem: 155977]

Dat kun je toch opsplitsen? Eerst zoek je alle varianten van strengen bij elkaar die opgeteld 870 geven. Dan heb je al een berg mogelijkheden verwijderd. Dan ga je ze in elkaar passen. Dan zijn er alweer een berg weg. Zo ga je door tot je steeds minder mogelijkheden hebt. Kun je zoiets niet bruut-forcen?

[Anoniem: 52509]

PiepPiep en MetalStef hebben het anders wel bij het rechte eind, Zyppora.

Als je na x aantal vakjes ingevuld te hebben kan schrappen, dan schakel je niet 1 mogelijkheid uit, maar (aantal vakjes - x)! mogelijkheden.

[Zyppora]

Argh! Je hebt gelijk ... en zij ook Naja, ere wie ere toekomt

Maar ik denk toch dat je, al had je distributed computing over een miljoen computers met elk een 3GHz dualcore ter beschikking, bij lange na niet binnen 300 jaar met alle mogelijkheden op een magisch vierkant kunt berekenen, zelfs niet als je met die tweak (aantal vakjes - x)! werkt. Het totaal aantal mogelijkheden is simpelweg te groot (ik bedoel, 10²⁴⁹ ... da's een 1 met 249 nullen!!)

[Anoniem: 58763]

Ik zou zeggen probeer het lekker zelf eens op te lossen m.b.v. een computer dan.

[DataGhost]

Je snapt dat je (denk ik, even vlug ) 144! mogelijkheden hebt? Calc zegt dat dat ongeveer
5,5502938327393047895510546605504e+249
mogelijkheden zijn. Als een computer er 6 miljard per seconde kan bruteforcen (3ghz dualcore?), ben je
9,250489721232174649251757767584e+239
seconden bezig, oftewel
2,931303306091773344377188939458e+229
millennia. Ongeveer.

Vergeet vooral de eisen waar het aan moet voldoen niet, het is al lastig zat om op elke rij 870 te krijgen. Vervolgens moet het diagonaal kloppen, diagonaal met een knik, in 'cirkel'vormen en bepaalde subgroepen moeten ook nog aan een stel eisen voldoen.

Mwah... anders ben ik even veel later dan Zyppora... met hetzelfde voorbeeld

[Zyppora]

Zelfs de proc is hetzelfde Knap van je

[OverSoft]

Is helemaal niet lastig, tenminste, niet als het alleen over diagonalen, horizontalen en verticalen mag gaan:
http://magie.nl.eu.org/magic.php?N=12&startgetal=1

[Rey Nemaattori]

Tijd voor kwamtumcomputers

[Bor]

Computer solved en de inhoud van de vakjes in hun hoofd gestampt met zijn 3-en?

[Sokratesz]

Het leuke van deze vierkanten is dat de algoritmes om ze te vullen bijna onmogelijk zijn te programmeren - en er dus nog gewoon lekker met de hand gewerkt wordt

[PiepPiep]

Ik zou het bijna vanavond als ik tijd heb gaan proberen te programmeren, ik zie namelijk nog niet echt wat er moeilijk aan is
Ik zie wel dat elke regel/kolom totaal 870 is, maar wat wordt er bedoelt met ‘eenderde Franklin magisch’?

[sewer]

Ik denk dat dit plaatje een boel verduidelijkt. http://www.brabantsdagbla...03_MagischVie_431218a.gif

Succes met programmeren

[Hanzy]

Het staat er toch echt:

dat het ‘eenderde Franklin magisch’ is, wat inhoudt dat de som van elke derde rij en derde kolom gelijk is aan 290.

[.oisyn]

Niet lastig nee, maar veel succes met het proberen van 144! =~ 5.55*10²⁴⁹ combinaties. Ik spreek je nog wel een keer als je op je sterfbed ligt en je algoritme nog niet eens 0.0001% van de totale ruimte heeft doorzocht

[marcieking]

Zo'n ding random invullen en checken of het aan alle voorwaarden voldoet?

Bruteforce FTW

[Anoniem: 194336]

Dan ben je waarschijnlijk jaren hetzelfde programma aan het uitvoeren vooraleer je er één gevonden hebt, tenzij je een BlueGene/L thuis hebt staan, als mediacenter ofzo...

[progster]

zou goed kunnen, een brute force oplosser van sudoku puzzels doet dit in minder dan 100ms...

[Anoniem: 172169]

Vermoedelijk wel ja.

[BtM909]

Overigens ook al een forum topic over: http://gathering.tweakers.net/forum/list_messages/1207291/0

Wellicht is dit plaatje ook nog interessant voor dit artikel: http://www.brabantsdagbla...03_MagischVie_431218a.gif

[Vincent7]

Iedereen die naar deze link -> http://magie.nl.eu.org/generator.html

verwijzen, dit is NIET de vierkant waar het artikel overgaat. De echte magische vierkant heeft nog meer voorwaarden dan alleen maar horizontale en diagonale optelling tot x.

BtM909 heeft een goede uitleg erover gevonden:

Overigens ook al een forum topic over: forum: Groter magisch vierkant ontdekt

Wellicht is dit plaatje ook nog interessant voor dit artikel: http://www.brabantsdagbla...03_MagischVie_431218a.gif

Ik denk toch echt niet dat men zo stom is dat ze denken dat er geen oplossing is, terwijl deze gewoon op het internet staat. Geef ze een beetje credit

EDIT: had cirkel ipv vierkant geschreven...

[Anoniem: 71510]

als auteur van http://magie.nl.eu.org/generator.html kan ik dat bevestigen :-)

wat deze jongens (en 1 meisje) in elkaar hebben gezet verdient zeker wel respect. Dit vind je echt niet met een beetje geluk, zoals sommigen suggereren.
Het enige wat ik heb gedaan met mijn website is een bestaand algoritme gebruiken in PHP-code. Dat is op zich niet echt speciaal

[Anoniem: 190966]

post je nou een link naar het forum waar mensen die er geen toegang tot hebben niet eens kunnen inzien??
beetje jammer ik was wel benieuwd naar wat er allemaal in dit topic vermeld stond?

dikke errors hier ej...

Error™

Er is iets fout gegaan. Probeer het later nog eens, of ga terug.

De gebruiker heeft geen toegang tot dit forum
(interne identificatie: forum::get_forumdata::forum_not_allowed)

[PaT]

en je bent wel ingelogd op GOT?

[Anoniem: 194589]

Om aan te geven hoeveel mogelijkheden er zijn om zo'n vierkant te vullen:

voor het eerste hokje : 144 (1 tot 144), 2e hokje (143), etc. Ofterwijl: 144! Gebruik maar eens een rekenmachine om dat uit te rekenen. Wellicht zijn er wel slimmere mogelijkheden maar met brute force schiet je weinig mee op.

[badflower]

ja zo maak je het wel heel makkelijk. Alleen gaat het niet zo op. Ik was nooit erg goed in dit soort dingen uitrekenen, maar je moet sowieso beginnen met 144! (144^144) min iets om de dubbele eruit te halen.

Dan hou je echt ongelooflijk veel mogelijkheden over om dat ding te vullen. Dus als het die kiddo's gelukt is, hebben ze een manier gevonden om het probleem op de een of andere manier op te splitsen in kleinere delen.

edit:
ahum, inderdaad lang geleden voor mij. 144! is natuurlijk ongelijk aan 144^144 Zie reactie stukje hieronder van michelkeijzers

[klaasvaag]

Het verhaaltje van michel klopt precies.

In het eerste hokje heb je 144 mogelijkheden, in het tweede ook, maar je gaat natuurlijk niet het getal invullen wat je in het vorige vakje al hebt ingevuld. 143 mogelijkheden dus..

Zo gaat dat door.. en uiteindelijk krijg je dus:
144 * 143 * 142 * ....... etc. etc.

En omdat dat nou eenmaal zoveel schrijfwerk is, hebben een paar slimme mensen verzonnen dat je dat kan schrijven als: 144!
En dat heet de 'faculteit van 144'

[Anoniem: 148116]

Dat is echt de meest idiote manier van bruteforcen. Een beetje programmeur bedenkt wel een betere algoritme met heel veel minder checks. Wat d8 je van een vergelijking opstellen voor elke hok. 144 vergelijkingen. Je kunt die 144 vergelijkingen makkelijk door een computer laten oplossen mbv matrixen. Dan moet je natuurlijk nog 1 hok varieren tussen 1 en 144. Dus 144 keer 144 vergelijkingen oplossen. Dit is echt binnen enkele seconden gedaan door een core duo. Maar natuurlijk weet ik niet of het werkt ik heb het zo even bedacht en ik ben niet van plan om het te gaan implementeren; ik heb wel wat beters te doen.

[Rey Nemaattori]

calc.exe zegt:
5,5502938327393047895510546605504*10^249 mogelijkheden.

Schien hadden ze een distributed client draaien met z'n drieën

[boner]

hoax of niet? zo maar precies 300 jaar na benjamin franklin?

Ik vermoed dat het met een brute force methode is gedaan.

[Anoniem: 209954]

Brute Force yeh right

144 vakjes die elk een waarde tot 144 kunnen bevatten:
dat is dus 144^144 = ong. 6.3 met 310 nullen erachter mogelijkheden. En in dit geval kan elk vakje elke waarde hebben tussen de 1 en 144.
Daarnaast moeten de vakjes zwel diagonaal, als horizontaal als verticaal en rondom de waarde 870 op leveren.

Daarnaast moet dus ook nog de som van elke derde rij en elke derde kolom gelijkstaan aan 290.

Ik wens je erg veel plezier dat te gaan brute forcen. Tot over een paar jaar

Dit geeft ook meteen het probleem weer om het uit te programmeren... de berekeningen zijn zo complex dat dit bijna niet te doen is.. ook niet om het uit te proberen.

( Rekenfouten voorbehouden )

[DarkTemple]

Je vergeet zoals zovelen heirboven, dat er gigantische bergen mogelijkheden afvallen, stel 1 rij voldoet niet, dan hoeven alle "weet ik veel hoeveel tig" mogelijkheden al niet meer bekeken te worden die er zijn voor de overige 11 rijen. Dit reduceert het gigantisch. Je moet alleen efficient programmeren.

[boner]

in principe zou je dan voor het 8 koninginnen probleem ook 8 boven 64 mogelijkheden hebben. Da's 4426165368
mogelijkheden. Met een beetje slim programmeren (eerste jaars informatica al) en wat doorlezen over recursie, en elke computer doet het binnen 1 seconde!

Ook magische vierkanten zijn te optimaliseren.

[ThE_ED]

Zeker gezien die "cirkelvormen" in het vierkant, denk ik ook aan een vroege 1 Aprilgrap.

[Anoniem: 171689]

Benjamin Franklin = 1709 geboren. Ik ga er met alle respect van uit dat zijn 8x8 vierkanten niet uit zijn 2e levensjaar komen..

[Anoniem: 93532]

Interessant, Op BNR newsradio hoorde ik dat het ging om een magisch vierkant met 16 vakjes dat ze zelf bedacht hebben.
In het artikel hierboven word gesproken over een magisch vierkant met 12 vakjes waarbij er in het vierkant nog een aantal dingen ontdekt zijn.

Op de website van de universiteit is helaas (nog) niks terug te vinden.

Dan maar jeugdjournaal of SBS6 kijken vanavond.

[Blaise]

Nou, even in de herhaling dan maar.
Het gaat om dit vierkant: http://www.brabantsdagbla...03_MagischVie_431218a.gif

[iTec]

Prachtig iedereen probeert het hier te verklaren, ik denk dat iedereen er naast zit , anders stonden ze nu wel naast die knakkers op de uni

[Vincent7]

Prachtig iedereen probeert het hier te verklaren, ik denk dat iedereen er naast zit

Precies wat ik denk. Tenzij iemand met compleet nieuwe ideeen komt, geef ik ze weinig kans. Ik bedoel, de gebruikelijke methoden zullen allemaal wel al geprobeerd zijn.

[twan1]

Is dit nu het bewijs dat het menselijk brein sneller rekent dan de snelste pc die we tot nu toe hebben ?

[gamepower2005]

Ik weet niet of je opmerking helemaal serieus bedoelt is, maar je hebt wel gelijk. Het brein is specifiek gemaakt voor bepaalde taken, maar kan die taken wel heel snel en goed verrichten. Daardoor zijn we ook veel beter in computers in het herkennen van plaatjes, en het bedenken van nieuwe ideeën. Het zou me ook niet verbazen als we de komende tijd nog wel beter blijven in bepaalde dingen dan computers.

Maar misschien is het programmeren van efficiënte programma's gewoon erg moeilijk voor dit soort problemen (of heeft niemand er de tijd voor genomen ).

[Limaad]

gaap plz?
pc's kunnen dit allaaaang...
als je er leuke vormpjes in wilt herkennen maak je daar er iets voor bij dat de pc daarop "let"...


http://magie.nl.eu.org/generator.html